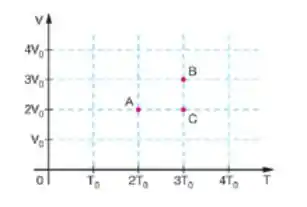
Os pontos A, B e C do gráfico, que representa o volume como função da temperatura absoluta (T), indicam três estados de uma mesma amostra de gás ideal. Sendo e as pressões correspondente aos estados indicados, é correto afirmar que:
- PA > PB > Pc
- PA > PB
- PA = PB > Pc
- PA = PB
- PA
Passo 1
E aí, galerinha! Tudo na paz por aí?
Po, o problema nos deu um gráfico de volume em função da temperatura (TV) e pede pra gente encontrar basicamente as relações de pressão.
Em propriedades termodinâmicas a gente tem sempre essas três propriedades atreladas, e o enunciado disse pra gente sobre ser uma amostra de gás ideal.
Palavrinha mágica: gás ideal.
Quando o enunciado falar isso, tem que vir na sua cabeça qual equação?
E vai ser a partir dessa equação que a gente vai avaliar cada pressão em seu respectivo estado.
Passo 2
Como queremos a pressão, vamos precisar isolar a pressão da nossa equação de estado:
Como o número de mols é constante pra um dado sistema fechado e R é a constante dos gases, vamos chamar esse produto .
Passo 3
Agora vamos avaliar o ponto A:
Ele está no volume e temperatura
Analogamente vamos fazer para o ponto B e C, show?
Passo 4
Opaaaa, concluímos aqui que e com isso já podemos eliminar as letras (A), (B) e (E).
Agora vamos avaliar
Note que , logo temos que
Portanto, a resposta correta é a letra (D)
Resposta
(D)