Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Gases Ideais

Ver Teoria
Exercício 512346789101112131415161718192021222324252627282930313233343536373839

Enunciado

Um recipiente A contêm um gás ideal à pressão de 5,0 × 10 5 P a e à temperatura de 300 K . Ele está conectado por um fino tubo com uma válvula a outro recipiente B , que tem quatro vezes o tamanho de A . O recipiente B contêm o mesmo gás ideal, à pressão de 1,0 × 10 5 P a e à temperatura de 400 K . A válvula de conexão é aberta e o equilíbrio é atingido a uma pressão comum, enquanto a temperatura de cada recipiente é mantida constante e igual ao seu valor inicial. Determine a pressão final do sistema.

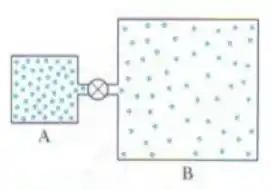
Dados:

V a = 1 l .

R = 8,31   J . m o l - 1 . K - 1

Passo 1

Bom, galera, uma boa estratégia para se resolver esse problema é se ligando nas propriedades do gás que serão constantes mesmo após ocorrer a abertura da válvula:

- A temperatura de cada recipiente. (Como diz o enunciado).

- O volume de cada recipiente, já que os recipientes que os contêm não se dilatarão.

- A quantidade total de mols.

Vamos deduzir a primeira relação que nos ajudará nessa questão:

Escrevendo a equação geral dos gases para o gás de A :

P A V A = n A R T A → n A = P A V A R T A

Após a abertura da válvula, a pressão passará a ser p ( Que é o que queremos achar). A gente pode escrever a expressão:

p V A = n A ' R T A   → n A ' = p V A R T A

Por que o número de mols passou a ser n A ' ? Bom, como a válvula foi aberta, o número de mols naquele recipiente muda, já que algumas moléculas podem escapar, ou mais moléculas podem entrar. Dividindo as duas equações:

n A ' n A = p V A R T A P A V A R T A

∴

n A ' n A = p P A

E essa é a expressão que nos ajudará. Podemos escrever a mesma coisa para o recipiente B :

n B ' n B = p P B

Passo 2

Vamos calcular os valores iniciais n A e n B :

n A = P A V A R T A   → n A = 5,0 × 10 5 . 10 - 3 8,31.300 ≅ 0,20056   m o l

Obs: Aqui temos que usar V A = 1 l = 10 - 3 m 3 em m 3 por que a nossa constante R tá no S.I.

Como V B = 4 V A , V B = 4 × 10 - 3 m - 3 :

n B = 1 × 10 5 × 4 × 10 - 3 8,31.400 ≅ 0,12034 m o l

Logo:

n = n A + n B = 0,20056 + 0,12034 = 0,32090   m o l

Passo 3

Agora vamos usar o fato de que o número total de m o l s é constante. Sendo:

n A ' = p V A R T A

E:

n B ' = p V B R T B

Logo:

n B ' n A ' = p V B R T B p V A R T A

→     n B ' n A ' = V B T A V A T B

∴

n B ' n A ' = 4 × 300 400 = 3  

→ n B ' = 3 n A '

Só que n A ' + n B ' = n . Logo:

n A ' + 3 n A ' = n  

→ n A ' = n 4

n A ' = 0,32090 4 ≅ 0,08022   m o l

Agora fica fácil (;

Vamos usar a expressão que achamos no início:

n A ' n A = p P A  

p = P A . n A ' n A  

p =   5,0 x 10 5 . 0,08022 0,200 5

∴

p ≅ 2,0 x 10 5 P a

Resposta

p =   2,0 x 10 5 P a

Exercícios de Livros Relacionados

60. Um frasco com volume de 1,50L , equipado com uma válvula, contém o gás etano ( C 2 H 6 ) a 300K e à pressão atmosférica ( 1,03 ⋅ 10 5P a ) . A massa molar do etanol é 30,1g / m o l . O sistema é a
Determine a massa em quilogramas de 7,50.10 24 átomos de arsênio, que tem uma massa molar de 74,9g / m o l .
Um pneu de automóvel tem um volume de 1,64.10 - 2m 3 e contém ar à pressão manométrica (pressão acima da pressão atmosférica) de 165k P a quando a temperatura é 0,00° C . Qual é a pressão manométrica
Uma amostra de oxigênio com um volume de 1000c m 3 a 40,0° C e 1,01.10 5P a se expande até um volume de 1500c m 3 a uma pressão de 1,06.10 5P a . Determine (a) o número de mols de oxigênio presentes n
Você copia o seguinte parágrafo de um livro de física marciano: "1 snorf de um gás ideal ocupa um volume de 1,35 Zaks. A uma temperatura de 22 glips, o gás tem uma pressão de 12,5 klads. A uma tempera