5) Hidrodinâmica.
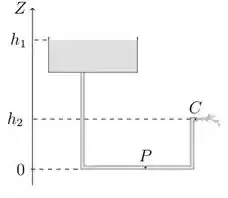
De um grande reservatório de água colocado a uma certa altura sai uma tubulação de seção reta constante que após atingir o nível do solo sobe um pouco e termina no ponto , como mostrado na figura. A superfície livre da água no reservatório está a uma altura do solo e o ponto está a uma altura do solo. Com a água jorrando livremente nesta extremidade do tudo, determine a pressão no ponto indicado na figura, que fica a parte da tubulação ao nível do solo. Desconsidere o efeito de contração da veia de líquido ao sair pela torneira. A área do reservatório é bem maior do que a da tubulação. A pressão do ar é .
a.
b.
c.
d. Não podemos determinar, pois não sabemos a velocidade no ponto
e.
f.
g.
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, essa questão deu pra gente um reservatório que está conectado com uma tubulação como na figura apresentada e pede pra que a gente descubra a pressão no ponto . E para fazer isso precisamos levar em consideração as energias envolvidas no escoamento da água que sai do reservatório e passa por toda essa tubulação até sair no ponto .
Vem comigo que te mostro como faremos isso.
Passo 2
Primeiro vamos nos lembrar que para situações desse tipo podemos aplicar a equação de Bernoulli. Então vamos escolher uma linha de corrente saindo da superfície da água no reservatório num ponto e percorra toda tubulação até atingir o ponto .
Assim, teremos:
Como tanto o reservatório quando a ponta do tuno no ponto estão em contato direto com atmosfera, podemos dizer que
E como o reservatório é muito grande em comparação a ponta da tubulação no ponto , podemos também dizer que as áreas se relacionam de modo que
E com isso a velocidade da água no ponto pode ser desprezada, uma vez que sua variação é muito pequena em comparação com a velocidade do ponto . Assim, dizemos que:
Com isso, nossa equação de Bernoulli se torna:
E isolando a velocidade no ponto , teremos:
Maravilha!
Agora vamos fazer a comparação do ponto com o ponto pedido pelo enunciado.
Passo 3
De maneira parecida, vamos considerar a Equação de Bernoulli, que será:
Por toda a tubulação não existe variação na largura do tudo, assim todas as seções retas do tubo são iguais, o que nos leva a:
O que nos dá:
O que faz os termos se cancelarem.
E a equação se torna:
Ainda podemos fazer
E isolando teremos:
Como é nossa referência, podemos toma-lo como nível zero e ficaremos com:
E encontramos nossa resposta, mostrando que a pressão no ponto pode ser calculado usando apenas o ponto como referência.
Resposta
Resposta:
a.