P2 de Álgebra Linear 1 da USP - 2016
Álgebra Linear 1 - USP
Em Mecânica, se são forças aplicadas, respectivamente, a pontos , define-se o momento desse sistema forças em relação a um ponto como sendo o vetor dado por:
Considere o sistema formado pelas forças
Aplicadas, respectivamente, aos pontos
E seja o momento desse sistema de forças em relação a um ponto . Assinale a alternativa correta:
existe um ponto tal que
o módulo do vetor é independente do ponto
para qualquer ponto , o vetor é uma combinação linear de e
se é um ponto que minimiza o módulo de , então não é uma combinação linear de e
se é um ponto que minimiza o módulo de , então e é uma combinação linear de e
Ver solução completaSejam vetores não nulos e e pontos do espaço . Considere o sistema de equações:
Na incógnita e as seguintes afirmações:
se e , então o sistema não tem solução;
se e , então o sistema tem infinitas soluções;
se , então o sistema tem uma única solução.
Assinale a alternativa correta:
apenas a afirmação é necessariamente verdadeira;
apenas as afirmações são necessariamente verdadeiras;
apenas as afirmações são necessariamente verdadeiras;
apenas a afirmação é necessariamente verdadeira;
todas as afirmações são necessariamente verdadeiras.
Ver solução completaConsidere o ponto , o plano
E a reta
Se é o ponto de tal que , então a soma das coordenadas de é igual a:
Ver solução completa
Considere as retas reversas
Se e são os pontos tais que a distância de a seja mínima, então é igual a:
Ver solução completa
Considere no espaço um cubo cujos vértices são em que são faces desse cubo, como ilustrado na figura abaixo:
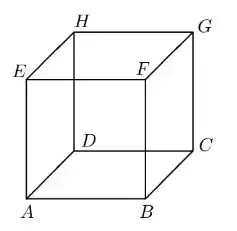
Seja e as bases de dadas por:
Se é a matriz real tal que
Para todo , então o determinante de é igual a:
Ver solução completa
Seja a reta que passa pela origem e é paralela ao vetor . Se é um ponto do plano
Tal que a distância de à reta seja igual a 1, então:
Ver solução completa
Considere os pontos , e a reta
Seja um plano tal que , a reta não intersecte e o ponto não pertença a . Se são tais que uma equação geral para é
Então é igual a
;
Ver solução completa
Considere a reta
E os pontos e Seja o ponto de tal que os ângulos e sejam congruentes. Temos que é igual a:
Ver solução completa
Considere os vetores , o plano
E a base de . Uma equação geral para o plano no sistema de coordenadas é:
Ver solução completa
Considere o plano e seja o ponto simétrico à origem em relação ao plano , isto é, o ponto tal que o vetor seja ortogonal a e o ponto médio do segmento esteja em . Temos que é igual a:
Ver solução completa
Considere as seguintes afirmações:
para quaisquer e quaisquer , vale que:
para quaisquer , vale que:
para quaisquer , vale que:
Assinale a alternativa correta:
apenas as afirmações e são verdadeiras
apenas a afirmação é verdadeira
apenas a afirmação é verdadeira
apenas as afirmações e são verdadeiras
apenas a afirmação é verdadeira
Ver solução completaConsidere o plano e as retas concorrentes
Se é o ponto na interseção de e , então a distância de ao plano é igual a:
Ver solução completa
Q5. Sejam um inteiro positivo, uma matriz real e uma matriz real . Considere o sistema linear , em que a matriz de incógnitas reais é . Pode-se afirmar que:
a) se o sistema possui solução, então ;
b) se o sistema não possui solução, então
c) se o sistema possui solução, então ;
d) se , então o sistema não possui solução;
e) se , então o sistema possui infinitas soluções.
Ver solução completa