Álgebra linear I, USP, P2, 2016, Questão 14
Considere no espaço um cubo cujos vértices são em que são faces desse cubo, como ilustrado na figura abaixo:
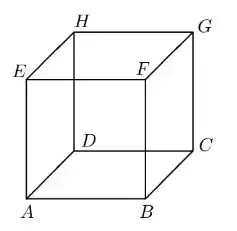
Seja e as bases de dadas por:
Se é a matriz real tal que
Para todo , então o determinante de é igual a:
Passo 1
Falaaaaa, beleza?? Bora lá para mais um probleminha dessa prova. Para entendermos o que vamos fazer bora analisar .
Essa equação nos diz que é a matriz que pega vetores escritos na base e transforma eles para base . Vale lembrarmos que quando temos uma matriz desse tipo, suas colunas são dadas por:
Coluna vetor de escrito na base
Coluna vetor de escrito na base
Coluna vetor de escrito na base
Ou seja, para montar a matriz, basta escrevermos cada cara da base como combinação dos vetores da base
Passo 2
Para fazermos isso, vamos notar que:
Ou seja:
Além disso, temos que:
Logo:
E para finalizar:
E por isso
Passo 3
Ou seja, temos que a nossa matriz é da forma:
Por Laplace, temos que:
E assim chegamos ao fim de mais um probleminha, bora para o próximo??
Resposta
Letra E