P1 de Álgebra Linear 1 da USP - 2021

Seja e considere a matriz dada por

A soma dos elementos na diagonal principal da matriz é igual a

a)

b)

c)

d)

e)

Com coordenadas dadas em relação a uma base fixada de , o vetor é combinação linear dos vetores e se, e somente se,

a)

b)

c)

d)

e)

Seja e considere o sistema linear homogêneo

Nas incógnitas reais e . Temos que esse sistema possui apenas a solução trivial se, e somente se

a)

b)

c)

d)

e)

Considere, em , o triângulo de vértices . Seja o ponto sobre o lado tal que e seja o ponto no segmento tal que . Seja o ponto sobre o lado que está na reta que passa por e , conforme a figura (fora de escala):

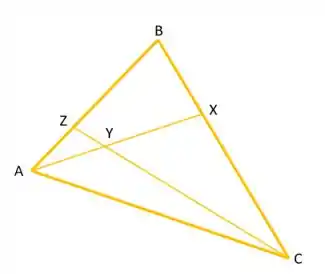
Se satisfaz , então é igual a

a)

b)

c)

d)

e)

f)

Sejam tais que

Então, é igual a

a)

b)

c)

d)

e)

Sabendo que e são vetores de tais que , o ângulo entre e mede e é ortogonal tanto a quanto a , é correto afirmar que é igual a

a)

b)

c)

d)

e)

f)

Seja uma base de e considere a base de , em que

Dado , as coordenadas de em relação à base são

a)

b)

c)

d)

e)

f)

g)

Sejam um inteiro maior ou igual a e uma matriz real . Considere as seguintes afirmações:

1. Se o determinante de é nulo, então existe uma linha de que é igual ao produto de alguma outra linha de por um número real

2. Se existe uma matriz real não nula tal que , então tem o determinante nulo

3. Se existe uma matriz real não nula tal que o produto não é inversível, então tem determinante nulo

a) Apenas 1 e 2 são verdadeiras

b) Apenas 1 e 3 são verdadeiras

c) Apenas 1 é verdadeira

d) Apenas 2 e 3 são verdadeiras

e) Apenas 2 é verdadeira

f) 1, 2 e 3 são verdadeiras

g) 1, 2 e 3 são falsas

h) Apenas 3 é verdadeira

Seja uma base ortonormal de . Considere os vetores e , em que são números reais. Sabendo que e que o ângulo entre e mede , é correto afirmar que é igual a

a)

b)

c)

d)

e)

f)

Considere fixada uma base ortonormal de em relação à qual são dadas coordenadas de vetores. Sejam

Seja o vetor que satisfaz as seguintes condições:

- tem norma

- é ortogonal a

-

- o ângulo entre e é agudo

Então, é igual a

a)

b)

c)

d)

e)

f)

Seja uma base de tal que

- ,

- o ângulo entre e mede

- é ortogonal tanto a quanto a

Considere os vetores e . Então, o produto escalar é igual a

a)

b)

c)

d)

e)

Seja e . Considere as seguintes afirmações sobre o sistema linear e sobre o sistema linear homogêneo associado :

1. Se tem infinitas soluções, então tem infinitas soluções

2. Se tem uma única solução, então só tem a solução trivial

3. Quando , é possível que só tenha a solução trivial e não tenha solução

a) Apenas 1 é verdadeira

b) Apenas 2 e 3 são verdadeiras

c) Apenas 3 é verdadeira

d) 1, 2 e 3 são falsas

e) 1, 2 e 3 são falsas

f) Apenas 1 e 2 são verdadeiras

g) Apenas 1 e 3 são verdadeiras

h) Apenas 2 é verdadeira

Seja uma base de e seja . O vetor é combinação linear dos vetores

Se, e somente se,

a)

b)

c)

d)

e)

f)

Sejam e bases de . Suponha que e que

Seja a matriz que satisfaz , para todo . Considere o vetor tal que . Sabendo que , é correto afirmar que o determinante de é igual a

a) 12

b) 24

c) 3

d)

e)

f)