P2 de Álgebra Linear 1 da USP - 2021

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

A distância entre o ponto e o plano

É

a)

b)

c)

d)

e)

f)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Considere a reta de equação vetorial

E a reta de equação simétrica:

A distância entre as retas e é igual a

a)

b)

c)

d)

e)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Considere o triângulo de vértices . O comprimento da bissetriz interna desse triângulo relativa ao vértice é

a)

b)

c)

d)

e)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Seja o plano de equação , e seja a reta de equações . Se o ponto de intersecção de e é o ponto médio do segmento , em que e , então é igual a

a)

b)

c)

d)

e)

f)

g)

h)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Seja . As retas

E

São reversas se, e somente se, é diferente de

a)

b)

c)

d)

e)

f)

Considere, em , o cubo de vértices e aresta unitária, conforme a figura

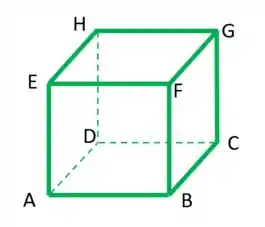
Suponha orientado de modo que a base seja positiva, e considere os vetores e . Então, as coordenadas, em relação à base , do produto vetorial são

a)

b)

c)

d)

e)

f)

g)

h)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva

Seja o plano que é paralelo às retas reversas

E

E que contém o ponto . Então, contém o ponto de coordenadas

a)

b)

c)

d)

e)

Considere fixada uma orientação de e seja uma base positiva de tal que e tal que seja ortogonal a e a . Suponha que , e que a medida do ângulo entre e seja igual a . Temos que é igual a:

a)

b)

c)

d)

e)

Sejam os vértices de um tetraedro cuja base é um triângulo de área igual a e cuja altura em relação a essa base tem comprimento igual a . Se

Então o volume do paralelepípedo determinado pelos vetores e é igual a

a)

b)

c)

d)

e)

Considere fixada uma orientação em . Sejam três vetores mutuamente ortogonais de norma 1. Considere as seguintes afirmações:

1. é uma base positiva se

2. Apenas uma das bases e é positiva

3. O volume do paralelepípedo definido pelos vetores é igual a

Então

a) Apenas 1 e 2 são verdadeiras

b) Apenas 3 é verdadeira

c) 1, 2 e 3 são verdadeiras

d) Apenas 2 é verdadeira

e) Apenas 1 é verdadeira

f) 1, 2 e 3 são falsas

g) Apenas 2 e 3 são verdadeiras

h) Apenas 1 e 3 são verdadeiras

Assuma orientado e considere coordenadas de pontos dados em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Seja a reta que passa pelo ponto e que é paralela à reta

São equações paramétricas de :

a)

b)

c)

d)

e)

f)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

A altura do tetraedro de vértices relativa à face é

a)

b)

c)

d)

e)

f)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Seja . A distância entre o ponto e o plano é menor ou igual a se, e somente se, pertence ao intervalo

a)

b)

c)

d)

e)