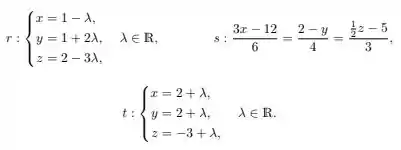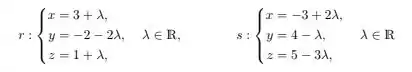P2 de Álgebra Linear 1 da USP - 2022

Sejam uma base ortonormal de e , vetores não nulos tais que

é paralelo a e é ortogonal a . Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam , vetores tais que o produto misto seja igual a . Temos que

é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e tais que

Se o ângulo entre e é obtuso, então é igual a:

(a)

(b)

(c)

(d)

(e)

Seja uma base ortonormal de e considere um triângulo em tal que:

Temos que o comprimento da altura desse triângulo relativa à base é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam , bases de e a matriz cujas colunas são , e . Se

E se é tal que e para certos , então é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e , e considere o vetor dado por

Se , , e a medida do ângulo entre e é igual a , então pode-se afirmar que:

(a) ou

(b) ou

(c) ou

(d) ou

(e) ou

Considere fixada uma orientação em . Seja um tetraedro em tal que:

E tal que a medida do ângulo entre os vetores e é igual a . Se a medida do ângulo entre os vetores e for igual a , então o volume desse tetraedro será igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas em . Sejam e e as retas dadas pelas equações:

Se e são concorrentes, então é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam e tais que , e . Suponha que a medida do ângulo entre e seja igual a e que a medida do ângulo entre e seja igual a . Temos que a projeção ortogonal de sobre é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam e bases de tais que

E seja a matriz tal que , para todo . Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Seja uma base ortonormal de e considere os vetores:

Se e é um triângulo em tal que e , então a área desse triângulo é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e com . Assinale a alternativa correta:

(a) se , então é ortogonal a

(b) se é ortogonal a , então

(c) o produto misto é nulo se, e somente se, é combinação linear de e

(d) se é linearmente dependente, então é paralelo a

(e)

Considere um sistema de coordenadas xado em e as retas e dadas pelas equações

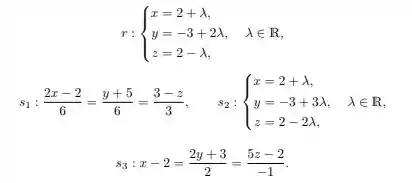
(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas , em que é uma base ortonormal de e sejam os pontos dados por

Seja a reta que passa pelo ponto e é ortogonal tanto à reta que passa pelos pontos como à reta que passa pelos pontos . Assinale a alternativa correspondente a uma equação para r:

(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas em . Sejam as retas

Assinale a alternativa correta:

(a) são paralelas distintas e são reversas

(b) são paralelas distintas e são concorrentes

(c) e são reversas

(d) são reversas e são concorrentes

(e) são reversas e são reversas

Considere fixado um sistema de coordenadas , em que é uma base ortonormal de . Sabe-se que as retas

são concorrentes. Seja a reta ortogonal a e a que passa pelo ponto de interseção entre . Assinale a alternativa correspondente a um ponto que pertence a :

(a)

(b)

(c)

(d)

(e)