P2 de Álgebra Linear 1 da USP - 2019

Considere o octaedro regular (isto é, cujas faces são triângulos equiláteros) de vértices , conforme a figura

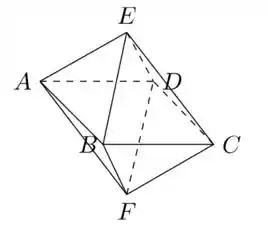
Sabendo que e que a segunda coordenada de é positiva, se é o plano que contém os pontos e é o ponto de mais próximo de , então é igual a

a) 6

b) 2

c) 5

d) 4

e) 3

Seja . Se a reta é paralela ao plano , então:

Seja um conjunto linearmente independente de três vetores em , e seja um ponto qualquer em . Considere os pontos , e . Então a área do triângulo de vértices é igual a:

Considere o plano de equação , e os pontos

Sejam as projeções ortogonais dos pontos sobre o plano . Qual das seguintes alternativas contêm as equações da reta que passa por ?

4. 2

Se tal que a interseção dos três planos

é uma reta, então está correto afirmar que:

A distância entre as retas

é:

Considere o prisma triangular reto (isto é, suas bases são triângulos e suas faces laterais retângulos) de vértices

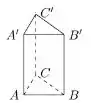
Sabe-se que e o volume do prisma é igual a . Se a primeira coordenada de é positiva ela é:

Sejam e considere as retas:

então são ortogonais se, e somente se:

Considere o ponto e o plano , definido por

Então, a distância do ponto ao plano é igual a

a)

b)

c)

d)

e)

Considere as seguintes afirmações sobre vetores arbitrários de :

I. A igualdade é necessariamente válida

II. Se , então

III. Se é linearmente independente e , então é uma base positiva

Está correto o que se afirma em

a) I,II e III

b) III, apenas

c) I e III, apenas

d) II, apenas

e) II e III, apenas

Se são tais que é a solução do sistema

Então o produto é igual a

a) 6

b) -24

c) 36

d) -8

e) 12

Dados os pontos e e os vetores e , com , considere as afirmações abaixo a respeito das retas e

I. As retas e são sempre reversas, para quaisquer valores de e

II. Se é o plano determinado pelo ponto e pela reta , então é ortogonal a se, se somente se,

III. A distância do ponto à reta é igual a

É correto afirmar que

a) I, II e III são verdadeiras

b) Apenas II e III são verdadeiras

c) Apenas I e III são verdadeiras

d) I, II e III são falsas

e) Apenas I e II são verdadeiras

O volume do tetraedro de vértices , em que , e , é igual a

a)

b)

c)

d)

e)

Seja uma base positiva de . Suponha que e que o vetor seja ortogonal a e a . Defina , e , e seja . Considere as seguintes afirmações:

I. é uma base ortogonal de

II. é uma base negativa de

III. Existe tal que

Está correto o que se afirma em

a) I, II e III

b) II e III, apenas

c) III, apenas

d) II, apenas

e) I, apenas

Seja a reta obtida pela interseção dos planos e . uma equação geral do plano que passa por e é perpendicular a reta é: