Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Produto Vetorial

Ver Teoria
Exercício 22123456789101112131415161718192021232425262728

Enunciado

USP; Álgebra Linear 1; P2 2019; questão 11

Seja   { u , v , w } um conjunto linearmente independente de três vetores em V 3 , e seja A um ponto qualquer em E 3 . Considere os pontos B   =   A + u , C   =   A + v e D   =   A + w . Então a área do triângulo de vértices B , C , D é igual a:

  1.   1 2 ( u ∙   u   + v ∙   v   + w ∙   w   )
  2. 1 2 | | u ∧ ( v ∧ w ) | |
  3. 1 2 | | u ∧ v + v ∧ w + w ∧ u | |
  4. 1 2 | | ( u - v ) ∧ ( ( v - w ) ∧ ( w - u ) ) | |
  5. 1 2 | [ u , v , w ] |

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Algelin!!! Dessa vez estaremos trabalhando com propriedades do produto vetorial. Vem comigo!!!

Nosso objetivo nessa questão é encontrar a área do triângulo de vértices B   =   A + u , C   =   A + v e D   =   A + w

Antes de começarmos a fazer essa questão, vamos revisar algumas propriedades do produto vetorial.

  1. x ∧ y   = - y ∧ x  
  2. x ∧ ( y + z )   =   x ∧ y   +   x ∧ z

Passo 2

Vamos encontrar a área do triângulo de vértices B   =   A + u , C   =   A + v e D   =   A + w .Mas a área de um triângulo cujas arestas são os vetores y   e   x é dada por 1 2   | | y   ∧   x | |         . Então vamos obter as arestas do nosso triângulo.

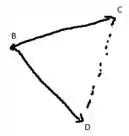
Elas serão:

x   =   B - C

= u - v

y = B - D

= u - w

Se prepara que lá vem conta, kkkk

Passo 3

Agora que temos nossas arestas vamos usar a fórmula da área, então

  A = 1 2   | | y   ∧   x | |        

= 1 2   | | u - v   ∧   u - w | |        

usando a propriedade 2 do enunciado

= 1 2   | | ( u - v   ∧   u ) + ( u - v   ∧ - w ) | |        

usando a propriedade 2 do enunciado

= 1 2   | | ( u ∧   u ) +   ( - v   ∧   u ) + ( u   ∧ - w ) +   ( - v   ∧ - w ) | |

usando a propriedade 1 do enunciado

= 1 2   | | 0 +   ( - u   ∧ -   v ) + ( w   ∧ u ) +   ( - v   ∧ - w ) | |

usando a propriedade 1 do enunciado 2 vezes seguidas

= 1 2   | |   ( u   ∧   v ) + ( w   ∧ u ) +   ( v   ∧ w ) | |

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

c)

Exercícios de Livros Relacionados

Se u é um vetor unitário, determine u . v e u . w
Um vendedor vende a hambúrgueres, b cachorros-quentes e c refrigerantes em um determinado dia. Ele cobra $2 o hambúrgues, $1,50 o cachorro-quente e $1 o refrigerante. Se A =a , b , c e P =2 ,1,5 ,1 ,
Para que valores de b os vetores - 6 , b , 2 e b , b^2 , b são ortogonais?
Calcule | u ×v | e determine se u ×v tem sentido de entrar ou sair da página.
Encontre o vetor, não com determinantes, mas usando propriedades do produto vetorial. k × ( i - 2 j )