Considere o prisma triangular reto (isto é, suas bases são triângulos e suas faces laterais retângulos) de vértices
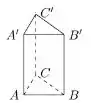
Sabe-se que e o volume do prisma é igual a . Se a primeira coordenada de é positiva ela é:
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de algelin.
Nosso objetivo é descobrir a primeira coordenada do ponto . e para isso nos é informado que e o volume do prisma é igual a . A primeira coordenada de é positiva.
Como vocês acham que podemos atacar esse problema? Vamos pensar um pouco

Passo 2
E ai, deu para pensar um pouco? Então vamos lá. O enunciado nos dá o volume do prisma, mas sabemos que o volume é a área da base vezes altura. Bem podemos calcular a área da base, e para obter a altura precisamos calcular o tamanho do vetor perpendicular à base (pois o prisma é reto). Veremos nos passos a seguir como encontramos esse vetor!!!!
Primeiro, vamos calcular a área da base. Como a base é um triângulo, a sua área será metade o módulo do produto vetorial dos vetores das arestas. isto é:
|/2
Vamos calcular .
Ao invés de calcularmos pela definição, podemos usar o fato que ele retorna um vetor ortogonal a e tentar chutar esse vetor. Como são vetores simples, é fácil verificar que o vetor
É ortogonal a

Agora que temos o vetor normal a base do prisma, podemos calcular a área da base.
|/2
Passo 3
No passo anterior, descobrimos que a área da base é
Mas o enunciado diz que o volume do prisma é . Como o volume do prisma é área da base vezes a altura, temos:
*
Opa, agora sabemos qual deve ser a altura do nosso prisma, mas qual vetor representa a altura???
O vetor ORTOGONAL a base do prisma!!!! Mas já sabemos quem é esse vetor. Que é:
mas precisamos de um vetor ortogonal a base que tenha tamanho . Isto é, queremos tal que:
Logo o vetor representa a altura do nosso prisma, pois tem tamanho e é ortogonal a base.
Passo 4
Agora, só precisamos descobrir quem é o ponto . Ora mas o prisma reto tem as bases paralelas, logo o ponto será dado pelo ponto mais o vetor da altura, isto é:
Logo
Que têm primeira coordenada igual a .

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊