USP Álgebra Linear 1 P2 2019
A distância entre as retas
é:
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez precisamos calcular a distância entre duas retas. Existe uma fórmula fechada, vocês lembram qual é? Bora revisar!!!
A distância entre duas retas é dada por:
Bacana, né? Vamos resolver a questão!!!
Passo 2
Como vimo no passo anterior, a distância entre duas retas é dada por:
Para podermos usar essa fórmula temos que escrever nossas retas na forma
Vamos começar pela reta , temos que:
Então:
e temos que:
Sendo assim, a nossa reta é dada por:
reescrevendo na forma
temos:
Passo 3
Agora vamos escrever dessa forma.
Para isso precisamos encontrar a solução do sistema
(vamos usar y de pivô)
Da primeira equação temos:
então
(da segunda equação)
então
Juntando esses resultados obtemos que:
que é equivalente a
Pronto, agora podemos usar a fórmula que revisamos no passo 1 para calcular a distância entre as retas!!!!
Passo 4
A fórmula é:
no nosso caso,
Então vamos começar calculando
Agora, precisamos obter
Vamos encontrar esse vetor. Para isso precisamos calcular o determinante da matriz
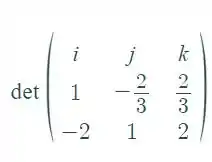
calculando o determinante obtemos:
Então nosso vetor é:
Passo 5
Agora temos tudo que precisamos para calcular a distância.
Então temos que:
e temos que
Então:
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊