Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.
A altura do tetraedro de vértices relativa à face é
a)
b)
c)
d)
e)
f)
Passo 1
E aí cara, tudo belezinha?
Vamos lá matar esse problema! Temos esse tetraedro:
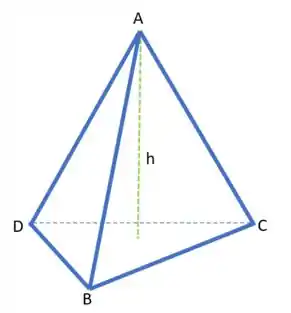
Onde
E aí queremos encontrar a altura em relação à base
Galera, a altura de um tetraedro em relação à base vai ser
Onde é o produto misto
Então vamos lá fazer esse cálculo 😉
Passo 2
A altura que queremos encontrar é calculada assim
Mas... quem são esses vetores ?? Não temos eles!!
Não mesmo! Mas temos os pontos
Então podemos encontrar os vetores:
Showw, vetores check
Passo 3
Vamos começar encontrando . Sabemos que
Esse produto misto é dado pelo determinante:
Calculando o determinante:
Showw! Então já temos o nosso numerador. Ele vale .
Passo 4
Agora vamos encontrar o denominador . Sabemos que e .
Esse produto vetorial é dado pelo determinante
Então
Showww! Esse é o vetor. O módulo dele vai ser
Ebaaa! Então já temos os valores para encontrar a altura
Passo 5
A altura do tetraedro vai ser
Substituindo os valores:
Então, a alternativa correta é a letra E 😊
Resposta
e)