USP – Álgebra Linear – P2 2021 – Questão 5
Sejam os vértices de um tetraedro cuja base é um triângulo de área igual a e cuja altura em relação a essa base tem comprimento igual a . Se
Então o volume do paralelepípedo determinado pelos vetores e é igual a
a)
b)
c)
d)
e)
Passo 1
Oiii, tudo belezinha? Vamos lá analisar essa geometria aí
Temos esse tetraedro:
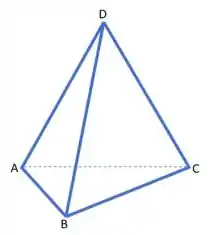
Onde o triângulo da base tem área igual a e a altura vale
E aí temos esses 3 vetores:
E queremos encontrar o volume do paralelepípedo definido por eles. Bom galera, o volume do paralelepípedo é dado pelo produto misto dos 3 vetores:
E outra informação que vamos usar pra chegar nesse volume é lembrar que o volume do tetraedro definido pelos vetores vai ser
Então vamos lá!
Passo 2
O volume do paralelepípedo definido pelos vetores vai ser
Mas sabemos que
Então:
Podemos separar em diferentes produtos mistos fazendo a distributiva:
E agora vamos lembrar do seguinte: se tivermos um produto misto com 3 vetores, mas um deles se repetir, então o produto misto vai ser 0, ok?
Então:
Colocando a constante pra fora:
Mas , então:
E portanto, o volume do paralelepípedo vai ser dado por
Legal, mas quem é ???
Vamos usar o volume do tetraedro para encontrar isso!!
Passo 3
Relembramos lá no passo 1 que o volume do tetraedro definido pelos vetores vai ser
No caso, sabemos que o volume do tetraedro também pode ser escrito como , onde é a área da base e é a altura
Então:
Show, então substituindo na equação ali de cima:
Uhuuu, então encontramos . Vamos substituir lá no volume do paralelepípedo
Passo 4
Lá do passo 2, temos que
E no passo 3, encontramos que
Então, o volume do paralelepípedo vai ser
E a alternativa correta é a letra B 😊
Resposta
b)