Considere, em , o cubo de vértices e aresta unitária, conforme a figura
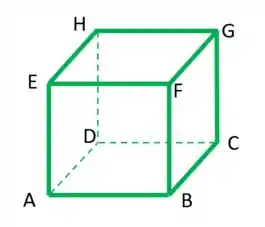
Suponha orientado de modo que a base seja positiva, e considere os vetores e . Então, as coordenadas, em relação à base , do produto vetorial são
a)
b)
c)
d)
e)
f)
g)
h)
Passo 1
Olááá galera, preparados pra mais uma?
Essa questão é o seguinte, ela dá dois vetores escritos na base :
E aí queremos as coordenadas de nessa mesma base
Aí a gente pensa “hahaha ué é só fazer o produto vetorial normal né?”
Nananinanão! O produto vetorial como a gente conhece é definido para bases ortonormais positivas. Mas a base não é ortonormal...Ela é formada pelos vetores , e :
Então aqui o esquema vai ser o seguinte:
- Vamos encontrar uma base nesse cubo que seja ortonormal e tenha algum tipo de relação com os vetores de (os vetores )
- Vamos encontrar as coordenadas de e na base
- Então, calculamos
- Por fim, escrevemos as coordenadas de na base novamente, e essa vai ser a resposta que buscamos, fechou?
Então vamos!
Passo 2
Vamos encontrar uma base ortonormal nesse cubo:
Podemos usar, por exemplo:
Porque é uma base bem próxima da base (lembrando que, geometricamente, )
A base é uma base ortonormal (os vetores são ortogonais e medem 1) e positiva. Então podemos usar essa base para calcular o produto vetorial de e
Passo 3
Para calcularmos o produto vetorial , precisamos primeiro encontrar os vetores e na base
Para isso, precisamos da matriz de mudança de base de para , a matriz . Para isso, basta colocarmos os vetores de escritos na base nas colunas de uma matriz
Vamos pensar nas coordenadas assim olha:
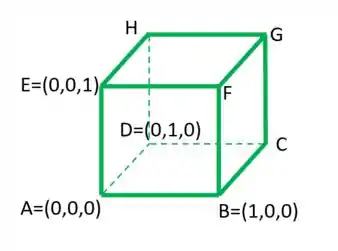
Como se realmente estivéssemos em e o ponto fosse a origem
Então, os vetores de escritos na base vão ser
E portanto, a matriz vai ser
Passo 4
Agora que temos a matriz de mudança de base, podemos encontrar e
Showww, então temos e
Agora vamos encontrar o produto vetorial entre eles
Passo 5
Já sabemos que e . Na base ortonormal , o produto vetorial vai ser
Então vamos calcular esse determinante:
Legal, então na base , o produto vetorial vai ser . Mas sabemos que . Então :
Opa opa opa!! Então escrevemos o produto vetorial de acordo com os vetores , que são os vetores da base :
Logo, na base temos que
Então a alternativa correta é a letra B!
Ufa, essa foi longa hahaha
Resposta
b)