Sejam subespaços do espaço vetorial
em que
e é o conjunto solução do sistema linear homogêneo:
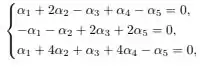
nas incógnitas reais . Assinale a alternativa correta:
(a) é um subespaço de
(b)
(c) .
(d)
(e)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Qual das afirmações a respeito dos subespaços
e é o conjunto solução do sistema linear homogêneo:
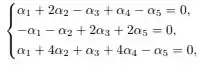
são verdadeiras. Bem para isso, vamos começar descobrindo quem é .

Passo 2
Para descobrirmos quem é , vamos resolver o sistema
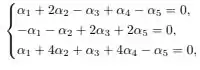
Fazendo ; temos:
Fazendo o sistema fica
Temos três equações e cinco variáveis, logo nosso sistema tem duas variáveis livres, vamos dizer que
, e . Logo
Resolvendo o sistema, obtemos que
Logo, temos as seguintes soluções para o sistema.
Ou seja, tem dimensão . E uma base para

Passo 3
Agora, vamos analisar , como
podemos observar que os vetores de são LI, log a dimensão de é . Mas o que podemos dizer de ?
Bem, a interseção são os vetores que estão em logo, temos que se
Mas note que
E que
Ou seja, podemos escrever os elementos da base de com os elementos da base de . Logo . Mas como vimos no passo anterior, tem a mesma dimensão. Isso implica que .
Portanto,
Que é um subespaço de . Logo a afirmação verdadeira é a alternativa

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊