USP; Sem campus; Álgebra Linear 2; P1; 2022; Questão 7
Considere os subespaços do espaço vetorial definidos por:
em que denota a transposta de uma matriz . Temos que é igual a:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Queremos descobrir a dimensão de , onde
Ou seja, são as matrizes simétricas e as matrizes onde seus elementos satisfazem .
Como fazemos isso? Ora, podemos achar uma base para . Vamos fazer isso
Passo 2
Passo 3
Passo 4
Se , então:
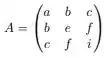
Mas se então
Ou seja, temos que
Logo, se , é da forma
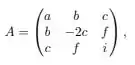
Passo 5
Descobrimos que se , é da forma
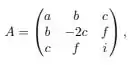
mas qual é a dimensão desse espaço? Bem, note que tem exatamente variáveis livres na matriz. Logo, a
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Exercícios de Livros Relacionados
Verifique se são espaços vetoriais os seguintes conjuntos:a) O R 2 com a adição usual e a multiplicação por escalar definida por α x , y = α x , 0 . b) O R 2 com x 1 , y 1 + x 2 , y 2 = ( x 1 + 2 x 2
Sejam X um conjunto não vazio e V um espaço vetorial. Mostre que, com as definições naturais de soma e multiplicação por escalar de funções, o conjunto das funções de X em V , F (X; V ), é um espaço v
Nos exercícios 5-6, em cada parte esboce, com ponto incial na origem, o vetor determinado pelos dois pontos dados.6 (a) P1(-1,0,2), P2(0,-1,0)
34 Seja P o ponto 1 ,3 ,7 . Se o ponto 4 ,0 ,- 6 for o ponto médio do segmento de reta que liga P e Q, quem é Q?
O problema apresenta um conjunto com as operações de adição e multiplicação por escalar nele definida. Verificar se é um espaço vetorial, e se não for, cite os axiomas que não se verificam. A = 0 a b