Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

P2 de Cálculo 4 da USP - 2018

Ver tudo sobre
Cálculo 4 - USP

Teste 1: O desenvolvimento em série de potências da função

f x = ∫ 0 x sin ⁡ t 2 t d t

Centrada no x = 0 é:

  1. ∑ n = 0 ∞ - 1 n t 4 n + 1 2 n + 1 ! 4 n + 1
  2. ∑ n = 0 ∞ - 1 n t 2 n + 1 2 n + 1 ! 2 n + 1
  3. ∑ n = 0 ∞ - 1 n t 4 n + 2 2 n + 1 ! 4 n + 2
  4. ∑ n = 0 ∞ - 1 n t 2 n + 2 2 n + 1 ! 4 n + 2

Ver solução completa

Teste 6: Se f x = x 2 sin ⁡ 2 x 2 , então sua derivada de ordem 2020 no zero, f 2020 0 , é:

  1. 2020 ! 1009 ! 2 1009
  2. - 2020 ! 1009 ! 2 2021
  3. - 2 1008 2020 !
  4. 2 1009

Ver solução completa

Teste 5: Sabe-se que

x 2 = π 2 3 + ∑ n = 1 ∞ - 1 n 4 n 2 cos ⁡ n x ,   0 < x < π

O valor de ∑ n = 1 ∞ 1 n 4 é:

  1. π 3 - π 72
  2. π 4 90
  3. π 2 24
  4. π 2 6 - 2 π 2 9

Ver solução completa

Teste 3: Sejam f x uma função periódica de período 2 tal que f x = 4 - 4 x para 0 ≤ x ≤ 1 e f x = f x + 1 para - 1 < x < 0 , e S x a soma da sua série de Fourier. Então S 0 , S - 3 e S 3 / 2 valem, respectivamente:

  1. 2 ,   2 ,   2
  2. 2 ,   0 ,   - 2
  3. 4 ,   0 ,   2
  4. 4 ,   0 ,   - 2

Ver solução completa

Questão 4: A soma da série

∑ n = 1 ∞ n 2 + 1 n x n

para x ∈ ] - 1 ,   1 [ é:

  1. - ln ⁡ 1 - x + x 1 - x 2
  2. ln ⁡ 1 - x + x 1 - x 2
  3. - ln ⁡ 1 - x - x 1 - x 2
  4. - ln ⁡ 1 - x + x 1 - x

Ver solução completa

Teste 2: Seja f x = 1 , para 0 ≤ x ≤ 1 2 e f x = - 1 , para 1 2 < x ≤ 1 . A série de cossenos de f é:

  1. ∑ n = 0 ∞ - 1 n 4 2 n + 1 π cos ⁡ 2 n + 1 π x
  2. ∑ n = 0 ∞ - 1 n + 1 4 n cos ⁡ n x
  3. ∑ n = 0 ∞ - 1 n + 1 4 n π cos ⁡ n π x
  4. ∑ n = 0 ∞ - 1 n 4 2 n + 1 cos ⁡ 2 n + 1 x

Ver solução completa

Teste 7: A integral

∫ 0 π 2 x - c 1 - c 2 cos ⁡ x 2   d x

Assume seu menor valor para c 1 e c 2 , respectivamente iguais a:

Ver solução completa

Teste 13: seja f : - 2 ,   2 → R uma função ímpar, C 1 por partes, com f 1 = 0 e cujo gráfico no intervalo 0 ,   2 está esboçado a seguir:

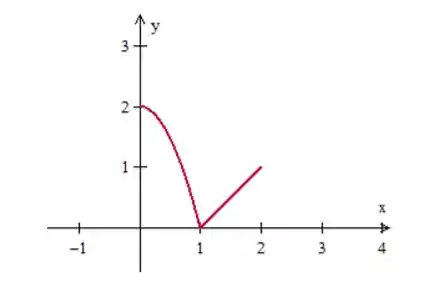
Sendo S x a soma da sua série de Fourier, analise as afirmações a seguir:

  1. S 2 n = 3 2 para todo n ∈ Z
  2. S x = S x + 2 para todo x ∈ R
  3. S x = f x para todo x ∈   ] 0 ,   2 [
  4. S n = 0 para todo n ∈ Z

Podemos afirmar que:

  1. Apenas 2 e 4 são verdadeiras.
  2. Apenas 1 e 2 são verdadeiras.
  3. Apenas 2 e 3 são verdadeiras.
  4. Apenas 3 e 4 são verdadeiras.

Ver solução completa

Teste 11: Seja f x = 1 2 - x para 0 , 1 2 e S x a soma da série de cossenos de f . No intervalo I = 7 2 , 9 2 , S x é dada por:

  1. S x = 1 2 - x
  2. S x = 1 2 - x + 8 2
  3. S x = 1 2 - x - 8 2
  4. S x = x - 8 2

Ver solução completa

Teste 14: A série de Taylor da função f x = 1 2 + x 2 centrada em x = 0 , e seu intervalo de convergência, são respectivamente:

  1. ∑ n = 0 ∞ - 1 n 2 n x 2 n ,         x ∈   ] - 1 2 ,   1 2 [
  2. ∑ n = 0 ∞ - 1 n x 2 n 2 n ,         x ∈   ] - 2 ,   2 [
  3. ∑ n = 0 ∞ - 1 n x 2 n 2 n + 1 ,         x ∈ - 2 ,   2
  4. ∑ n = 0 ∞ - 1 n x 2 n 2 n + 1 ,         x ∈   ] - 2 ,   2 [

Ver solução completa

Teste 12: Seja a função

f x = 2 x 2 - x + 1 ,         0 ≤ x ≤ π   2 x 2 + x - 1 ,     - π ≤ x ≤ 0

A soma S x da série de Fourier de f no intervalo - π ,   π é:

  1. S x = 2 x 2 - x + 1 ,         0 < x < π 2 x 2 + x - 1 ,     - π < x < 0 0 ,                                               x = 0 2 π 2 ,                                   x = ± π
  2. S x = 2 x 2 - x + 1 ,         0 ≤ x < π 2 x 2 + x - 1 ,     - π < x < 0 2 π 2 - π ,                                   x = ± π  
  3. S x = 2 x 2 - x + 1 ,         0 < x ≤ π 2 x 2 + x - 1 ,     - π ≤ x < 0 0 ,                                               x = 0  
  4. S x = 2 x 2 - x + 1 ,         0 < x < π 2 x 2 + x - 1 ,     - π < x < 0 0 ,                                               x = 0 2 π 2 - π ,                                   x = ± π

Ver solução completa

Teste 10: A soma da série

∑ n = 0 ∞ x + 2 n n + 2 !

Par x ∈ R e x ≠ - 2 é:

  1. 1 x + 2 e x + 2 - 1
  2. 1 x + 2 2 e x + 2
  3. 1 x + 2 2 e x + 2 - 1 - x + 2 - x + 2 2 2
  4. 1 x + 2 2 e x + 2 - 1 - x + 2

Ver solução completa

Questão 9: A soma da série

∑ n = 2 ∞ n n + 1 3 n

É...

a ) 19 12

b ) 17 12

c ) 18 12

d ) 20 12

Ver solução completa

Teste 8: Sejam f x = arctan ⁡ x e

g x = ∑ n = 0 ∞ - 1 n x 2 n + 1 2 n + 1

  1. f x = g x para todo x ∈ R .
  2. O domínio da g x está contido no intervalo - 5 ,   4 .
  3. f n 0 = g n 0 para todo n natural
  4. lim x → ∞ ⁡ g x = π 2
  5. f 2 π 0 = 1 2 π

Podemos afirmar que:

  1. Apenas 2 e 3 são verdadeiras.
  2. Apenas 3 e 4 são verdadeiras.
  3. Apenas 1 , 3 e 4 são verdadeiras.
  4. Apenas 2 , 3 e 5 são verdadeiras.

Ver solução completa

Listas de Exercícios Resolvidos

P2 - 2019P2 - 2016P2 - 2015P3 - 2014P1 - 2020P3 - 2017P2 - 2010P3 - 2018P-SUB - 2017P-REC - 2018