![]()
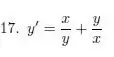
Passo 1
Para testar se é uma EDO homogênea mesmo, temos que pegar o e o da nossa EDO e substituir por e respectivamente. Se a EDO não mudar, ela é homogênea. Então nesse caso
Fazendo a substituição
A EDO permanece a mesma, logo ela é homogêna.
Passo 2
Agora, para resolver vamos utilizar a substituição
E vamos precisar de
Fazendo a substituição
Manipulando um pouco nossa expressão
Repare que a EDO se tornou separável
E para resolver basta integrar dos dois lados da equação
Passo 3
Resolvendo a integral
Já do outro lado a expressão
Note que teremos constantes de integração dos dois lados da equação, mas para facilitar a vida, é melhor juntar em apenas uma constante .
Passo 4
Resolvidas as integrais, vamos juntar tudo na mesma expressão
Manipulando mais um pouco chegaremos em
Agora podemos desfazer aquela substituição lá do inicio
E ficamos com
Prontinho!
Resposta
