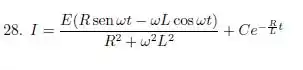Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelagens com Fator Integrante

Ver Teoria
Exercício 1112345678910121314151617181920212223242526272829

Enunciado

Passo 1

Para começar, vamos dividir toda a nossa EDO por L:

d I ( t ) d t + R L I t = E L sen ⁡ w t

Perceba que essa é uma EDO de primeira ordem linear, então vamos resolver daquele jeito clássico.

A t = R L B t = E L sen ⁡ w t

Passo 2

Precisamos calcular a integral ∫ A t d t sem adicionar a constante e achar I t = e ∫ A t d t

∫ A t d t = ∫ R L d t = R L t

Assim ficou:

∫ A t d t = R L t

I t = e ∫ A t d t

I t = e R L t

Passo 3

Agora vamos calcular a integral ∫ I t ⋅ B ( t ) d t

∫ E L sen ⁡ w t e R L t d t

E L ∫ sen ⁡ ( w t ) e R L t d t

Essa integral pode ser resolvida utilizando integração por partes:

∫ sen ⁡ ( w t ) e R L t d t

Chamamos de :

w = e R L t → d w = R L e R L t d z = sen ⁡ w t d t → z = - 1 w cos ⁡ w t

Assim:

∫ sen ⁡ ( w t ) e R L t d t = - 1 w e R L t cos ⁡ w t + R w L ∫ cos ⁡ w t e R L t d t

∫ cos ⁡ w t e - R L sen ⁡ t d t = ?

Mesma coisa:

w = e R L t → d w = R L e R L t d z = cos ⁡ w t → z = 1 w sen ⁡ w t

∫ sen ⁡ ( w t ) e R L sen ⁡ t d t = - 1 w e R L t cos ⁡ w t + R w L 1 w e R L t sen ⁡ w t - R w L ∫ sen ⁡ w t e R L t d t

Perceba que a integral que apareceu na esquerda é igual à da direita, então podemos passar ela para o mesmo lado e colocar ela em evidência:

1 + R 2 w 2 L 2 ∫ sen ⁡ ( w t ) e - R L t d t = - 1 w e R L t cos ⁡ w t + R w 2 L e R L t sen ⁡ w t

Assim:

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = - 1 w e R L t cos ⁡ w t 1 + R 2 w 2 L 2 + R w 2 L e R L t sen ⁡ w t 1 + R 2 w 2 L 2

Ta ficando enorme mesmo mas vamos lá:

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = - w L 2 e R L t cos ⁡ w t w 2 L 2 + R 2 + R L   e R L t sen ⁡ w t w 2 L 2 + R 2

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = e R L t w 2 L 2 + R 2 R L sen ⁡ w t - w L 2 cos ⁡ w t

Então:

E L ⋅ e R L t w 2 L 2 + R 2 ( R L sen ⁡ w t - w L 2 cos ⁡ w t )

Vamos tentar dar uma ajeitada pra ficar com uma aparência melhor:

V 0 e R L t w 2 L 2 + R 2 R sen ⁡ w t - wLcos ⁡ w t

E e R L t ⋅ w L w 2 L 2 + R 2 R w L sen ⁡ w t - cos ⁡ w t

Passo 4

Então qual é a cara da solução?

i t = 1 I t ∫ I t ⋅ B t d t + C

i ( t ) = E e R L t ⋅ w L w 2 L 2 + R 2 R w L sen ⁡ w t - cos ⁡ w t ⋅ e - R L t + C e - R L t

i ( t ) = E R sen ⁡ w t - w L cos ⁡ w t R 2 + w 2 L 2 + C e - R L t

Resposta

Exercícios de Livros Relacionados

24. Um trenó foguete, com velocidade inicial de 150 milhas/h (≈ 240 km/h), é freado por um canalde água. Suponha que, enquanto está sendo freado, a aceleração a do trenó é dada por a(υ) = –μυ², em que
19. Considere um lago, de volume constante V, contendo, no instante t, uma quantidade Q(t) de poluentes distribuídos uniformemente em todo o lago com uma concentração c(t), onde c(t) = Q(t)/V. Suponha
24. Um trenó foguete, com velocidade inicial de 150 milhas/h (≈ 240 km/h), é freado por um canalde água. Suponha que, enquanto está sendo freado, a aceleração a do trenó é dada por a(υ) = –μυ², em que
6. Suponha que um tanque contendo determinado líquido tem uma saída próxima do fundo. Seja h(t) a altura da superfície do líquido acima da saída no instante t. O princípio de Torricelli2 diz que a vel
6. Suponha que um tanque contendo determinado líquido tem uma saída próxima do fundo. Seja h(t) a altura da superfície do líquido acima da saída no instante t. O princípio de Torricelli2 diz que a vel