Exercícios Mais Acessados UTFPR - Halliday Vol 3 - 9°ed de Física 3 da UTFPR - Campo Elétrico

(Cap 22 Ex – 3) O núcleo de um átomo de plutônio 239 contém 94 prótons. Suponha que o núcleo é uma esfera com 6,64 fm de raio e que a carga dos prótons está distribuída uniformemente na esfera. Determine (a) o módulo e (b) o sentido (para dentro ou para fora) do campo elétrico produzido pelos prótons na superfície do núcleo.

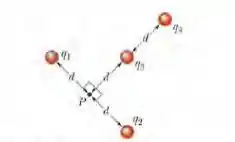
(Cap 22 Ex – 8) Na Fig. 22-31, as quatro partículas são mantidas fixas e têm cargas = = +Se, = +3e e = - 12e. A distância d= 5,0 μm. Qual é o módulo do campo elétrico no ponto P?

(Cap 22 Ex – 1) Faça um esboço das linhas de campo elétrico entre duas cascas esféricas condutoras concêntricas e do lado de fora da casca de maior raio supondo que existe uma carga positiva uniforme na casca de menor raio e uma carga negativa uniforme na casca de maior raio. Considere os casos , e .

(Cap 22 Ex – 4) Duas partículas são mantidas fixas no eixo x: a partícula 1, de carga , no ponto x = 6,00 cm, e a partícula 2, de carga , no ponto x = 21,0 cm. Qual é o campo elétrico total a meio caminho entre as partículas, em termos dos vetores unitários?

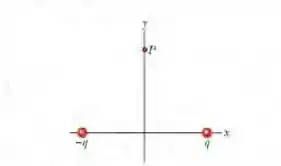
(Cap 22 Ex – 9) A Fig. abaixo mostra duas partículas carregadas mantidas fixas no eixo x: , no ponto x = - 3,00 m, e , no ponto x = +3,00 m. Determine (a) o módulo e (b) a orientação ( em relação ao semieixo x positivo) do campo elétrico no ponto P, para o qual y = 4,00 m.

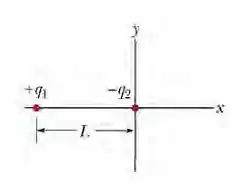
(Cap 22 Ex – 10) A primeira figura mostra duas partículas carregadas mantidas fixas no eixo x a uma distância L uma da outra. A razão entre os valores absolutos das cargas das duas partículas é 4,00. A segunda figura mostra a componente x, do campo elétrico no eixo x, à direita da partícula 2, em função de x. A escala do eixo x é definida por = 30,0 cm, que é o último valor indicado no gráfico. (a) Para que valor de x > 0 o valor de , é máximo? (b) Se a carga da partícula 2 é = - 3e, qual é o valor do campo máximo?

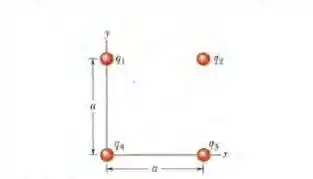
(Cap 22 Ex – 7) Na Fig. abaixo, as quatro partículas formam um quadrado de Iado a = 5,00 cm e têm cargas = + 10,0 nC, = -20,0 nC, = + 20,0 nC e = -10,0 nC. Qual é o campo elétrico no centro do quadrado, em termos dos vetores unitários?

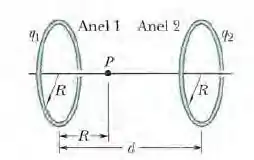
(Cap 22 Ex – 23) A Fig. abaixo mostra dois anéis não condutores paralelos, com o centro na mesma reta perpendicular aos planos dos anéis. O anel 1, de raio R, possui uma carga uniforme ; o anel 2, também de raio R, possui uma carga uniforme . Os anéis estão separados por uma distância d = 3,00R. O campo elétrico no ponto P da reta que passa pelos centros dos anéis, que está a uma distância R do anel 1, é zero. Calcule a razão .

(Cap 22 Ex - 81) Existe na atmosfera um campo elétrico Ê, dirigido verticalmente para baixo, cujo módulo é da ordem de 150 N/C. Estamos interessados em fazer "flutuar" nesse campo uma esfera de enxofre com 4,4 N de peso carregando-a eletricamente. (a) Qual deve ser a carga da esfera (sinal e valor absoluto)? (b) Por que o experimento não pode ser realizado na prática?

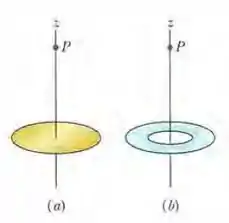
(Cap 22 Ex – 37) Um engenheiro foi encarregado de projetar um dispositivo no qual um disco uniformemente carregado de raio R produz um campo elétrico. O módulo do campo é mais importante em um ponto P sobre o eixo do disco, a uma distância 2,00R do plano do disco (figura a). Para economizar material, decidiu-se substituir o disco por um anel com o mesmo raio externo R e um raio interno R/2,00 (figura b). O anel tem a mesma densidade superficial de cargas que o disco original. Qual é a redução percentual do módulo do campo elétrico no ponto P?

(Cap 22 Ex - 67) Uma corda com uma densidade linear uniforme de cargas de é estendida ao longo do eixo x . Determine o módulo do campo elétrico no ponto do eixo x .

(Cap 22 Ex – 50) Em um certo instante, as componentes da velocidade de um elétron que se move entre duas placas paralelas carregadas são e . O campo elétrico entre as placas é dado por . Em termos dos vetores unitários, determine (a) a aceleração do elétron; (b) a velocidade do elétron no instante em que sua coordenada x variou de 2,0 cm.

(Cap 22 Ex – 19) A Fig. abaixo mostra um dipolo elétrico. Determine (a) o módulo e (b) a orientação ( em relação ao semieixo x positivo) do campo elétrico produzido pelo dipolo em um ponto P Situado a uma distância

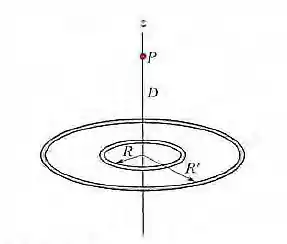
(Cap 22 Ex – 30) A Fig. Abaixo mostra dois anéis concêntricos, de raios R e R' = 3,00R, que estão no mesmo plano. O ponto P está no eixo central z, a uma distância D = 2,00R do centro dos anéis. O anel menor possui uma carga uniformemente distribuída + Q. Em termos de Q, qual deve ser a carga uniformemente distribuída no anel maior para que o campo elétrico no ponto P seja nulo?

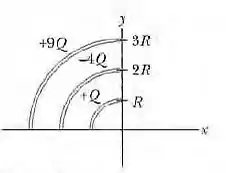
(Cap 22 Ex – 25) A Fig. abaixo mostra três arcos de circunferência cujo centro está na origem de um sistema de coordenadas. Em cada arco, a carga uniformemente distribuída é dada em termos de Q = 2,00 μC. Os raios são dados em termos de R = 10,0 cm. Determine (a) o módulo e (b) a orientação ( em relação ao semieixo x positivo) do campo elétrico na origem.

(Cap 22 Ex – 48) Na figura abaixo, um elétron (e) é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio R. A densidade superficial de cargas do disco é. Determine o módulo da aceleração inicial do elétron se for liberado a uma distância (a) R, (b) R/100, (c) R/1000 do centro do disco. (d) Por que o módulo da aceleração quase não varia quando o elétron está próximo do disco?

(Cap 22 Ex - 66) Um próton e um elétron ocupam dois vértices de um triângulo equilátero de lado m. Qual é o módulo do campo elétrico no terceiro vértice do triângulo?

(Cap 22 Ex – 15) Na Fig. abaixo, as três partículas são mantidas fixas no lugar e têm cargas = = +e e = +2e. A distância a= 6,00 μ,m. Determine (a) o módulo e (b) a direção do campo elétrico no ponto P.

(Cap 22 Ex – 52) Um elétron penetra, com uma velocidade inicial de , em uma região na qual existe um campo elétrico uniforme de módulo , e se move paralelamente ao campo. (a) Qual é a velocidade do elétron 1,5 ns depois de entrar na região? (b) Que distância o elétron percorre nesse intervalo de 1,5 ns?

(Cap 22 Ex – 35) A que distância ao longo do eixo de um disco de plástico uniformemente carregado de 0,600 m de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?

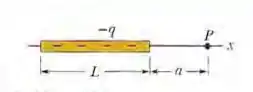
(Cap 22 Ex – 31) Na Fig. abaixo, uma barra não condutora de comprimento L = 8,15 cm tem uma carga - q = -4,23 fC uniformemente distribuída. (a) Qual é a densidade linear de cargas da barra? Determine (b) o módulo e (c) a direção (em relação ao semieixo x positivo) do campo elétrico produzido no ponto P, situado no eixo x, a uma distância a = 12,0 cm da extremidade da barra. Determine o módulo do campo elétrico produzido em um ponto situado no eixo x, a uma distância a = 50 m do centro da barra, (d) pela barra e (e) por uma partícula de carga -q = -4,23 fC colocada no lugar anteriormente ocupado pelo centro da barra.

(Cap 22 Ex – 11) Duas partículas são mantidas fixas sobre o eixo x: a partícula 1, de carga , no ponto x = 20 cm, e a partícula 2, de carga , no ponto x = 70 cm. Em que ponto do eixo x o campo elétrico total é nulo?

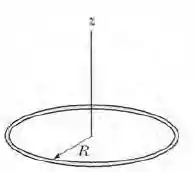
(Cap 22 Ex – 24) Uma barra fina não condutora, com uma distribuição uniforme de carga positiva Q, tem a forma de uma circunferência de raio R fig. abaixo. O eixo central do anel é o eixo z, com a origem no centro do anel. Determine o módulo do campo elétrico (a) no ponto z = 0 e (b) no ponto z = . (c) Em termos de R, para que valor positivo de z o módulo do campo é máximo? (d) Se R = 2,00 cm e Q = 4,00 μC, qual é o valor máximo do campo?

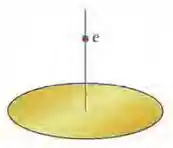
(Cap 22 Ex – 13) A Fig. abaixo mostra um próton (p) no eixo central de um disco com uma densidade uniforme de cargas devido a um excesso de elétrons. Três dos elétrons são mostrados na figura: o elétron no centro do disco, e os elétrons , em extremidades opostas do disco, a uma distância R do centro. O próton se encontra inicialmente a uma distância z = R = 2,00 cm do disco. Com o próton nessa posição, determine o módulo (a) do campo elétrico produzido pelo elétron e (b) do campo elétrico total produzido pelos elétrons . O próton é transferido para o ponto z = R/10,0. Determine os novos valores (c) do módulo de e (d) do módulo de . (e) Os resultados dos itens (a) e (c) mostram que o módulo de aumenta quando o próton se aproxima do disco. Por que, nas mesmas condições, o módulo de diminui, como mostram os resultados dos itens (b) e (d)?