Exercícios Mais Acessados UTFPR - Halliday Vol 3 - 9°ed de Física 3 da UTFPR - Lei de Gauss

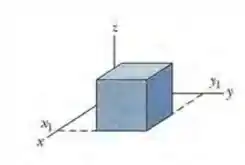
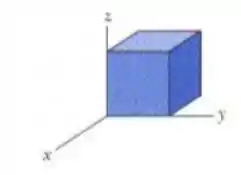
(Capítulo 23.4 – Exercício 6) Em todos os pontos da superfície do cubo da Fig. 23-27, o campo elétrico é paralelo ao eixo z. O cubo tem 3,0 m de aresta. Na face superior do cubo, ; na face inferior,. Determine a carga que existe no interior do cubo.

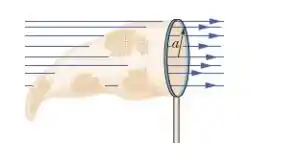
(Capítulo 23.4 – Exercício 4) Na Fig. 23-28, uma rede para pegar borboletas está imersa em um campo elétrico uniforme de módulo . O plano do aro da rede, uma circunferência de raio , é mantido perpendicular à direção do campo. A rede é eletricamente neutra. Determine o fluxo elétrico através da rede.

(Capítulo 23.4 – Exercício 7) Uma carga pontual de está no centro de uma superfície Gaussiana cúbica de 55 cm de aresta. Qual é o fluxo elétrico através da superfície?

(Capítulo 23.4 – Exercício 8) Quando um chuveiro é aberto em um banheiro fechado, os respingos de água no piso do boxe podem encher o ar de íons negativos e produzir um campo elétrico no ar de até 1000 N/C. Considere um banheiro de dimensões 2,5 m X 3,0 m X 2,0 m. Suponha que no teto, no piso e nas quatro paredes o campo elétrico no ar é perpendicular à superfície e possui um módulo uniforme de 600 N/C. Suponha também que o teto, o piso e as paredes formam uma superfície gaussiana que envolve o ar do banheiro. Determine (a) a densidade volumétrica de cargas ρ e (b) o número de cargas elementares e em excesso por metro cúbico de ar.

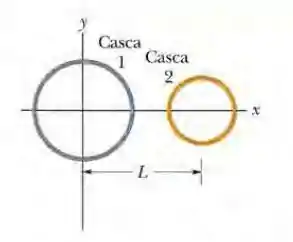
(Capítulo 23.4 – Exercício 12) A Fig. 23-32 mostra duas cascas esféricas não condutoras mantidas fixas no lugar. A casca 1 possui uma densidade superficial de cargas uniforme de +6,0 μC/m2 na superfície externa e um raio de 3,0 cm; a casca 2 possui uma densidade superficial de cargas uniforme de +4,0 μC/m 2 na superfície externa e um raio de 2,0 cm; os centros das cascas estão separados por uma distância L = 10 cm. Em termos dos vetores unitários, qual é o campo elétrico no ponto x = 2,0 cm?

(Capítulo 23.4 – Exercício 11) A Fig. 23-31 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, com um vértice no ponto x1 = 5,00 m, y1 = 4,00 m. O cubo está imerso em um campo elétrico dado por, com y em metros. Qual é a carga total contida no cubo?

(Capítulo 23.6 – Exercício 17) Uma esfera condutora uniformemente carregada com de diâmetro possui uma densidade superficial de cargas . (a) Determine a carga da esfera. (b) Determine o fluxo elétrico através da superfície da esfera.

(Cap 23 Ex- 2) Um campo elétrico dado por E = 4,0î – 3,0(y2 + 2,0)ĵ atravessa um cubo gaussiano com 2,0 m de aresta, posicionado da forma mostrada na Fig. 23-5. (E é dado em Newtons por coulomb e x em metro .) Determine o fluxo elétrico (a) através da face superior; (b) através da face inferior; (c) através da face da esquerda; (d) através da face traseira. (e) Qual é o fluxo elétrico total através do cubo?

(Cap 23 Ex- 3) O cubo da Fig. 23-27 tem 1,40 m de aresta e está orientado da forma mostrada na figura em uma região onde existe um campo elétrico uniforme. Determine o fluxo elétrico através da face direita do cubo, se o campo elétrico, em Newtons por coulomb, é dado por (a) (d) Qual é o fluxo total através do cubo nos três casos?

(Capítulo 23.4 – Exercício 13) Observa-se experimentalmente que o campo elétrico em uma certa região da atmosfera terrestre aponta verticalmente para baixo. A uma altitude de 300 m, o campo tem um módulo de 60,0 N/C; a uma altitude de 200 m, o módulo é 100 N/C. Determine a carga em excesso contida em um cubo com 100 m de aresta e faces horizontais a 200 e 300 m de altitude.

(Capítulo 23.7 – Exercício 27) Um fio reto longo possui cargas negativas fixas com uma densidade linear de . O fio é envolvido por uma casca coaxial cilíndrica, não condutora, de paredes finas, com de raio . A casca possui uma carga positiva na superfície externa, com uma densidade superficial , que anula o campo elétrico do lado de fora da casca. Determine o valor de .

(Capítulo 23.4 – Exercício 10) A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de de aresta, imersa em um campo elétrico dado por, com em metros. Qual é a carga total contida no cubo?

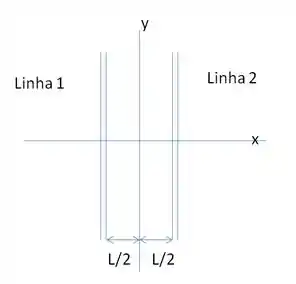
(Capítulo 23.7 – Exercício 30) Na Fig. 23-39, pequenas partes de duas linhas paralelas de cargas muito compridas são mostradas, fixas no lugar, separadas por uma distância . A densidade uniforme de cargas das linhas é para a linha e para a linha . Em que ponto do eixo o campo elétrico é zero?

(Capítulo 23.7 – Exercício 24) A Fig. 23-36 mostra uma seção de um tubo longo de metal, de paredes finas, com um raio e uma carga por unidade de comprimento . Determine o módulo do campo elétrico a uma distância radial (a) ; (b) . (c) Faça um gráfico de em função de para .

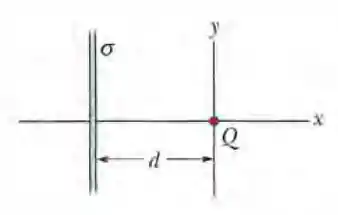
(Capítulo 23.8 – Exercício 40) A Fig. 23-46 mostra uma placa não condutora muito extensa que possui uma densidade superficial de cargas uniforme ; a figura mostra também uma partícula de carga , a uma distância da placa. Ambas estão fixas no lugar. Se , para que coordenada (a) positiva e (b) negativa sobre o eixo (além do infinito) o campo elétrico total , é zero? (c) Se , para que coordenada sobre o eixo x o campo

é zero?

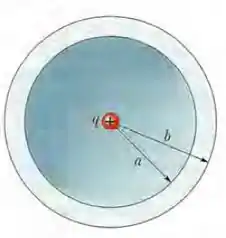
(Capítulo 23 – Problemas Adicionais – Exercício 70) Uma esfera não condutora com 5,0 cm de raio possui uma densidade volumétrica uniforme de cargas . Determine o módulo do campo elétrico (a) a 3,5 cm e (b) a 8,0 cm do centro da esfera.

(Capítulo 23.9 – Exercício 51) Na Fig. 23-52, uma casca esférica não condutora com um raio interno e um raio externo possui uma densidade volumétrica uniforme de cargas positivas , onde é uma constante e ré a distância em relação ao centro da casca. Além disso, uma pequena esfera de carga está situada no centro da casca. Qual deve ser o valor de para que o campo elétrico no interior da casca () seja uniforme?

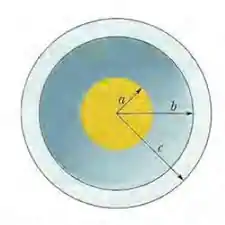
(Capítulo 23.9 – Exercício 45) Duas cascas esféricas concêntricas carregadas têm raios de 10,0 e. A carga da casca menor é e a da casca maior é . Determine o campo elétrico (a) em ; (b) em .

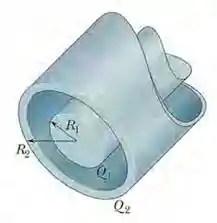
(Capítulo 23.7 – Exercício 31) A Fig. 23-38 é uma seção de uma barra condutora de raio e comprimento no interior de uma casca coaxial, de paredes finas, de raio e mesmo comprimento . A carga da barra é ; a carga da casca é . Determine (a) o módulo e (b) a direção (para dentro ou para fora) do campo elétrico a uma distância radial . Determine (c) e (d) a direção do campo elétrico para . Determine a carga (e) na superfície interna e (f) na superfície externa da casca.

(Capítulo 23.9 – Exercício 55) Uma distribuição de cargas não uniforme, mas com simetria esférica, produz um campo elétrico de módulo , onde é uma constante e r é a distância do centro da esfera. O campo aponta para longe do centro da esfera. Qual é a distribuição volumétrica de cargas ?

(Capítulo 23 – Problemas Adicionais – Exercício 73) Uma esfera não condutora tem uma densidade volumétrica de cargas uniforme . Seja r o vetor que liga o centro da esfera a um ponto genérico P no interior da esfera. (a) Mostre que o campo elétrico no ponto P é dado por . (Observe que o resultado não depende do raio da esfera.) (b) Uma cavidade esférica é aberta na esfera, como mostra a Fig. 23-56. Usando o princípio da superposição, mostre que o campo elétrico no interior da cavidade é uniforme e é dado por , onde é o vetor que liga o centro da esfera ao centro da cavidade.

(Capítulo 23 – Problemas Adicionais – Exercício 65) Uma carga Q está distribuída uniformemente em uma esfera de raio R. (a) Que fração da carga está contida em uma esfera de raio r = R/2,00? (b) Qual é a razão entre o módulo do campo elétrico no ponto r = R/2,00 e o campo elétrico na superfície da esfera?

(Capítulo 23 – Problemas Adicionais – Exercício 76) Um cilindro muito longo de raio R possui uma distribuição volumétrica de cargas uniforme. (a) Mostre que, a uma distância r E = ρ r 2 ϵ 0 , em que é a densidade volumétrica de cargas. (b) Escreva uma expressão para E do lado de fora do cilindro.

(Capítulo 23.7 – Exercício 32) Um cilindro maciço, longo, não condutor, com de raio, possui uma densidade volumétrica de cargas não uniforme que é função da distância radial a partir do eixo do cilindro: . Se , determine o módulo do campo elétrico (a) para ; (b) para

(Capítulo 23.9 – Exercício 53) Uma esfera não condutora de raio possui uma distribuição de cargas não uniforme , onde é a distância do centro da esfera. (a) Determine a carga da esfera. Determine o módulo do campo elétrico (b) em ; (c) em ; (d) em (e) Faça um gráfico de E em função de .

(Capítulo 23.9 – Exercício 52) A Fig. 23-53 mostra uma casca esférica com uma densidade volumétrica de cargas uniforme , raio interno e raio externo . Determine o módulo do campo elétrico (a) em ; (b) em ; (c) em ; (d) em ; (e) em ; (f) em .

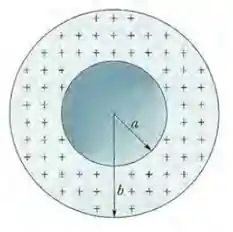
(Capítulo 23.9 – Exercício 49) Na Fig. 23-50, uma esfera maciça de raio é concêntrica com uma casca esférica condutora de raio interno e raio externo . A esfera possui uma carga uniforme e a casca possui uma carga . Determine o módulo do campo elétrico

em ;

em ;

em ;

em ;

em ;

em .

Determine a carga

na superfície interna e

na superfície externa da casca.