Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 4 - Problema 15.
(Cap 22 Ex – 15) Na Fig. abaixo, as três partículas são mantidas fixas no lugar e têm cargas = = +e e = +2e. A distância a= 6,00 μ,m. Determine (a) o módulo e (b) a direção do campo elétrico no ponto P.
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
O enunciado nos fala que tem uma configuração igual a da figura de 3 partículas e ele quer saber o módulo e a direção do campo elétrico no ponto P.
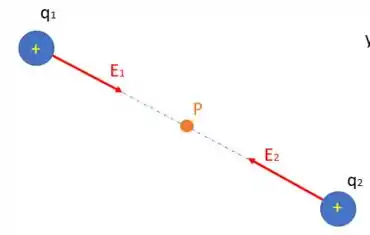
Primeiramente, devido a simetria, e pelas cargas das partículas 1 e 2 serem iguais, notamos que a contribuição do vetor campo elétrico devido a essas partículas se anulam:
Passo 2
Então, só precisamos calcular a contribuição devido a partícula 3. Assim, o problema fica bem mais reduzido:
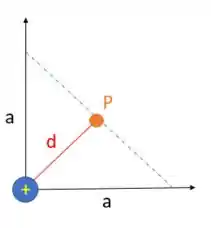
Lembrando que a distância da partícula 3 até o ponto P é igual a metade da diagonal de um quadrado de lado , que é:
Passo 3
Item (a)
Para calcular o módulo do campo elétrico devido a partícula 3, devemos usar a equação do campo elétrico:
Onde:
- é a distância entre a carga e o ponto onde ela gera o campo elétrico;
- é o valor da carga e
- é uma constante que vale:
Considerando que só queremos o módulo, vamos usar o módulo da carga 3:
Substituindo a distância que encontramos:
Elevando o denominador ao quadrado:
Ajeitando essa fração:
Substituímos então , a carga elementar e a constante :
Elevando o denominador ao quadrado:
Passo 4
Item (b)
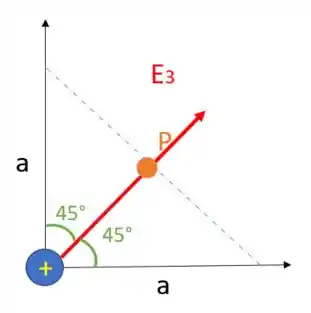
O vetor campo elétrico está na direção ponto P e partícula 3, pois como apenas o campo gerado pela partícula 3 impacta o campo elétrico total no ponto P, o campo total terá a direção do campo da carga 3. Mas qual é a direção desse campo?
Vamos pensar que como a carga 3 é positiva, as linhas de campo apontam para fora, logo o vetor campo elétrico faz um ângulo de 45° com o semieixo positivo x:
