Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 4 - Problema 8.
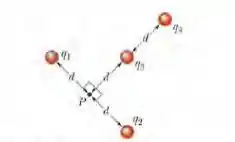
(Cap 22 Ex – 8) Na Fig. 22-31, as quatro partículas são mantidas fixas e têm cargas = = +Se, = +3e e = - 12e. A distância d= 5,0 μm. Qual é o módulo do campo elétrico no ponto P?
Passo 1
Falaaaai galerinha, show de bola? Bora resolver mais uma juntinho comigo?
Simboráaa
O enunciado nos fala de quatro partículas com carga e ele quer saber o módulo do campo elétrico no ponto P.
Primeiro, uma maneira mais simples de solucionar esse problema é colocar a origem do sistema de coordenadas no ponto P e o eixo y na direção da partícula 4 (passando pela partícula 3).
Assim, escolheremos também o eixo x perpendicular ao eixo y, passando pelas partículas 1 e 2.
Lembre-se da fórmula do cálculo do campo elétrico de uma carga pontual:
Em que é a constante de Coulomb ( é a distância da partícula até o ponto em que estamos calculando e é a carga da partícula.
Passo 2
Note que o módulo do campo elétrico produzido pelas partículas 1 e 2 se cancelam, pois elas estão a mesma distância do ponto P e possuem cargas iguais.
Então, só temos que calcular o módulo do campo elétrico no eixo y.
Como as partículas 3 e 4 possuem cargas de sinais diferentes, basta que a gente calcule o módulo e subtraia uma da outra, nesse caso, colocaremos o sinal de menos na partícula 3, pois o campo produzido por ela terá sentido contrário ao eixo y.