(Cap 22 Ex – 11) Duas partículas são mantidas fixas sobre o eixo x: a partícula 1, de carga , no ponto x = 20 cm, e a partícula 2, de carga , no ponto x = 70 cm. Em que ponto do eixo x o campo elétrico total é nulo?
Passo 1
Falaaaaaaaaa galerinha do Responde ai, tudo joinha?
Bora resolver essa juntinho comigo?
Simboráaa
O enunciado nos fala que existem duas partículas de cargas de sinais opostos que estão situadas no eixo x e ele quer saber qual posição do eixo x o campo elétrico total é nulo.
Primeira coisa que devemos saber é que as linhas do campo elétrico de uma carga positiva apontam para fora:
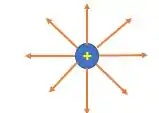
Enquanto cargas negativas geram linhas de campo elétrico que apontam pra dentro:
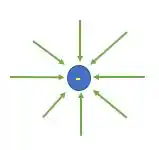
Logo, o campo produzido por elas é como na figura:
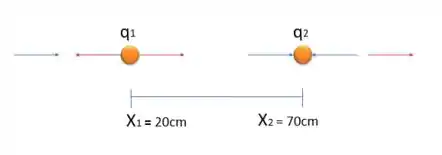
Bem, como as partículas 1 e 2 têm cargas de sinais opostos, em pontos que estão no meio delas o campo elétrico não se anula, ele irá se somar.
Passo 2
Como a carga da partícula 2 é maior em módulo do que a carga da partícula 1, então o ponto que tem campo elétrico nulo tem que está mais afastado da partícula 2 do que da 1. Então o ponto tem que ser à esquerda da partícula 1:
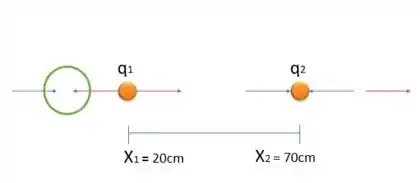
Passo 3
Chamaremos de a coordenada no eixo x do ponto em que o campo elétrico é nulo. Então, calculando o módulo do campo elétrico:
Onde:
- é constante;
- é a carga que gera o campo elétrico e
- é a distância entre o ponto onde foi gerado o campo e a carga geradora.
Logo, o campo gerado pela carga 1 será:
Enquanto o campo gerado pela carga 2 será:
Onde é o ponto onde desejamos calcular o campo elétrico nulo!
Passo 4
Lembrando que o campo gerado pela partícula 1 é divergente, e como o ponto está à esquerda dela, o vetor campo elétrico está no sentido contrário ao crescimento do eixo x:
Para que o campo seja nulo, , então:
Substituindo os valores de e
Lembrando que :
Passo 5
Tirando a raiz quadrada e deixando essa equação na forma direta:
Vamos por opção:
- Se:
- Se:
Então:
Como esse ponto deve estar à esquerda da partícula 1, a solução deve ser .