Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Uniforme

Ver Teoria
Exercício 25123456789101112131415161718192021222324262728293031323334353637383940414243444546

Enunciado

Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 7 - Problema 35.

(Cap 22 Ex – 35) A que distância ao longo do eixo de um disco de plástico uniformemente carregado de 0,600 m de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?

Passo 1

E ai seres de luz, tudo bem?

Bora resolver mais uma?

Encostaaa!!

Para essa questão, temos que saber a fórmula de cálculo do campo elétrico de um disco de raio R a uma distância z   dele. Você lembra? Essa fórmula está na eq. 22-26 do livro e também aqui embaixo:

E = σ 2 ϵ 0 1 - z z 2 + R 2  

Em que:

  • σ   é a densidade superficial de cargas;
  • z é a distância no eixo do disco;
  • R é o raio do disco.

Veja a imagem abaixo:

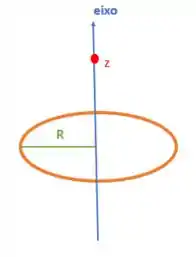
Passo 2

O campo elétrico no centro do disca ( z = 0 ) é

E C = σ 2 ϵ 0 1 - 0 0 2 + R 2  

E C = σ 2 ϵ 0 1 - 0

E C = σ 2 ϵ 0

Passo 3

Desejamos achar um ponto z em que o módulo do campo elétrico seja igual à metade do módulo do campo no centro do disco isto é:

E = 1 2 E C

Temos:

E = 1 2 σ 2 ϵ 0

E =   σ 4 ϵ 0

Substituindo E pela fórmula geral que usamos no passo 1:

σ 2 ϵ 0 1 - z z 2 + R 2   = σ 4 ϵ 0

Vamos cancelar a densidade linear de carga σ que temos dos dois lados:

1 2 ϵ 0 1 - z z 2 + R 2   = 1 4 ϵ 0

Multiplicando os dois lados por 2 ϵ 0 :

1 - z z 2 + R 2   = 1 2

Passo 4

Agora vamos passar a expressão que contem z só para um lado

    1 - 1 2 = z z 2 + R 2  

z z 2 + R 2   = 1 2

2 z =   z 2 + R 2  

Elevando os dois lados ao quadrado:

4 z 2 = z 2 + R 2

3 z 2 = R 2

Tirando a raiz quadrada dos dois lados da equação:

z = R 3

Substituindo o valor de R = 0,600 m :

z = 0,600 m 3

Obtemos nossa resposta assim:

z = 0,346   m

Resposta

z = 0,346   m

Exercícios de Livros Relacionados

Na Fig. abaixo, duas barras curvas de plástico, uma de carga +q e outra de carga -q, formam uma circunferência de raio R = 8,50 cm no plano xy . O eixo x passa pelos dois pontos de ligação entre os ar
Verdadeiro ou falso:O campo elétrico de uma carga puntiforme sempre aponta no sentido que se afasta da carga. A força elétrica em uma partícula carregada em um campo elétrico é sempre na mesma direção
Na Fig. 22-45, duas barras curvas de plástico, uma de carga + q e outra de carga - q , formam uma circunferência de raio R = 8,50c m no plano x y . O eixo x passa pelos dois pontos de ligação entre os
Duas placas horizontais muito grandes estão a uma distância de 4,25c m uma da outra e possuem densidade de cargas iguais, porém contrárias, de módulo σ . Você quer usar essas placas para manter fixa n
Repita o problema 21.100 considerando que a placa B é positiva.