Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 4 - Problema 10.
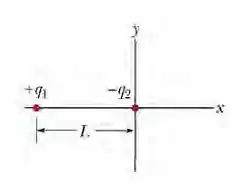
(Cap 22 Ex – 10) A primeira figura mostra duas partículas carregadas mantidas fixas no eixo x a uma distância L uma da outra. A razão entre os valores absolutos das cargas das duas partículas é 4,00. A segunda figura mostra a componente x, do campo elétrico no eixo x, à direita da partícula 2, em função de x. A escala do eixo x é definida por = 30,0 cm, que é o último valor indicado no gráfico. (a) Para que valor de x > 0 o valor de , é máximo? (b) Se a carga da partícula 2 é = - 3e, qual é o valor do campo máximo?
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Bom, nós temos duas cargas de sinais opostos que irão causar um campo do lado direto da partícula 2, certo?
Vamos colocar em um desenho:
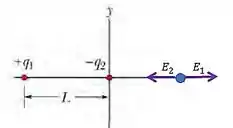
Vamos assumir que este campo está a uma distância x da origem, ok?
Teremos então um campo resultante sendo aplicado neste ponto, que podemos escrever assim:
Se lembram como calculamos o campo elétrico?
Bom, olhando lá no gráfico que o problema nos deu nós conseguimos achar as distâncias da carga 1 e 2:
Substituindo na equação acima:
Colocando os termos em evidência, vamos ter que:
Lembrando que:
Então:
Passo 2
Nós precisamos achar o L, certo? E para isso vamos olhar no gráfico e ver que quando o campo sera :
Tirando a raiz:
Passo 3
Boom, agora nós precisamos achar o valor de x cujo campo é máximo!
Do cálculo nós sabemos que para achar um ponto máximo derivamos a função e igualamos a zero.
Bora fazer isso??
Já achamos a letra (a) !!
Passo 4
Agora nós só precisamos achar a letra (b)!!
Ela nos diz que:
E para que o campo seja máximo:
Substituindo tudo na equação do campo:
E chegamos ao fim !!