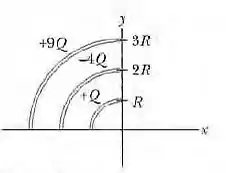
(Cap 22 Ex – 25) A Fig. abaixo mostra três arcos de circunferência cujo centro está na origem de um sistema de coordenadas. Em cada arco, a carga uniformemente distribuída é dada em termos de Q = 2,00 μC. Os raios são dados em termos de R = 10,0 cm. Determine (a) o módulo e (b) a orientação ( em relação ao semieixo x positivo) do campo elétrico na origem.

Iremos chamar o raio menor de , o raio do arco do meio de e o raio do arco maior de .

Então, o comprimento do arco menor é:

o comprimento do arco do meio é:

E o comprimento do arco maior é:

Como a carga no arco está uniformemente distribuída, podemos calcular a densidade linear de carga dos três arcos:

E:

Item (a)

Para esse item, utilizaremos a fórmula do campo elétrico de um arco de circunferência carregado (se quiser a dedução dessa fórmula, encontra-se no início do capítulo 22 deste livro):

Em que é a densidade linear de carga.

No caso dessa questão, como na questão o arco faz , então . Somando os campos dos três arcos:

Resolvendo esse carnaval aí o resultado fica:

Substituindo e temos:

Item (b)

Ao olharmos para a figura, vemos que não é necessário nenhum cálculo para saber qual o ângulo do vetor campo elétrico. Basta a gente perceber qual o eixo de simetria dos arcos: -45° em relação ao semieixo positivo x.

Assim, basta perceber que todas as componentes do campo elétrico que não estão nessa direção se cancelarão, pois todo ponto do arco acima desse eixo de simetria irá ter uma componente que irá se cancelar pelo ponto simétrico na parte debaixo do arco.

Assim, o campo faz um ângulo de com o semieixo x positivo.