Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 4 - Problema 9.
(Cap 22 Ex – 9) A Fig. abaixo mostra duas partículas carregadas mantidas fixas no eixo x: , no ponto x = - 3,00 m, e , no ponto x = +3,00 m. Determine (a) o módulo e (b) a orientação ( em relação ao semieixo x positivo) do campo elétrico no ponto P, para o qual y = 4,00 m.
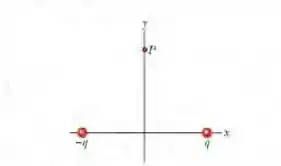
Passo 1
Falaaaai meus amores?
Como estão??
Vem comigo que eu tenho um plano, no caminho eu explicoooo!
Shooow galerinha, vamos para mais uma questão beeem legal !!
Antes de qualquer coisa nós vamos aplicar os campos que estão chegando lá no ponto P, ok? Na carga o campo é apostado para ela, enquanto para a o campo aponta para longe! Como a distância até a origem é a mesma, teremos o mesmo ângulo.
Agora é só desenhar:
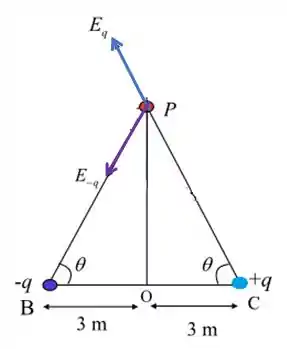
Como as forças são angulares, elas terão componentes nas direções x e y:
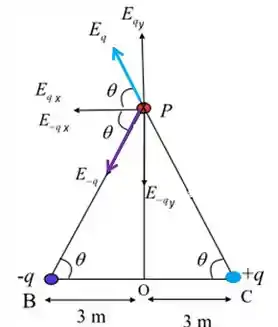
Passo 2
Bom, o campo elétrico é calculado por uma fórmula:
Se é uma constante, o campo elétrico depende somente da carga e da distância entre elas e o ponto P.
Então, o campo elétrico produzido por elas terá a mesma intensidade, porém direções diferentes, ocasionadas pelas cargas positivas e negativas.
Olhando na figura acima podemos concluir que:
Novamente no desenho nós vemos que o campo resultante será:
Isso aqui já responde a letra (b), certo? Nós temos um campo resultante sendo apontado na direção negativa de x !!
E agora nós podemos seguir para a letra (a) !!
Passo 3
Bom, se lembrarmos da trigonometria da coisa:
Então:
Substituindo o campo:
E o que nós temos aqui? Quase nada:
Nós precisamos de e do cosseno, certo?
Passo 4
O é a hipotenusa do triângulo retângulo formado entre uma das cargas e o ponto P, e é calculada como:
O cosseno também é possível calcular olhando este mesmo triângulo:
Agora sim !!
É só colocar na fórmula:
Chegamos ao fim de mais umaa !!
Resposta
a)
b) O campo elétrico aponta no sentido negativo de x.