Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Carga Pontual

Ver Teoria
Exercício 4912345678910111213141516171819202122232425262728293031323334353637383940414243444546474850515253545556575859606162636465666768697071727374757677787980818283848586878889909192

Enunciado

Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção 6 - Problema 30.

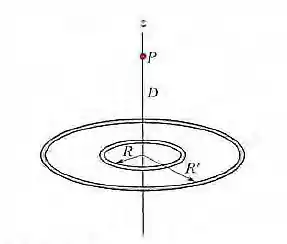
(Cap 22 Ex – 30) A Fig. Abaixo mostra dois anéis concêntricos, de raios R e R' = 3,00R, que estão no mesmo plano. O ponto P está no eixo central z, a uma distância D = 2,00R do centro dos anéis. O anel menor possui uma carga uniformemente distribuída + Q. Em termos de Q, qual deve ser a carga uniformemente distribuída no anel maior para que o campo elétrico no ponto P seja nulo?

Passo 1

E ai seres de luz, tudo bem?

Bora resolver mais uma?

Encostaaa!!

Nós temos que lembrar da fórmula do campo elétrico devido a um anel de raio R   a uma distância z   do anel que é:

E = q z 4 π ϵ 0 z 2 + R 2 3 2  

Logo o anel interno causa o seguinte campo:

E i n t = ( 2 R ) Q 4 π ϵ 0 ( 2 R ) 2 + R 2 3 2

Enquanto o anel externo causa o seguinte campo e queremos achar a carga q :

E e x t = 2 R q 4 π ϵ 0 ( 2 R ) 2 + ( 3 R ) 2 3 2

Passo 2

Somando os campos devido aos dois anéis que queremos que seja nula:

E t o t = ( 2 R ) Q 4 π ϵ 0 ( 2 R ) 2 + R 2 3 2 + 2 R q 4 π ϵ 0 ( 2 R ) 2 + ( 3 R ) 2 3 2 = 0

Resolvendo essa equação:

2 R Q 4 π ϵ 0 5 R 2 3 2 + 2 R q 4 π ϵ 0 13 R 2 3 2 = 0

2 R 4 π ϵ 0 Q 5 R 2 3 2 + q 13 R 2 3 2 = 0

Q 5 R 2 3 2 + q 13 R 2 3 2 = 0

q 13 R 2 3 2 = - Q 5 R 2 3 2

Obtemos como resposta:

q =   - Q 13 5 3 2 =   - 4,19 Q

Resposta

q =   - 4,19 Q

Exercícios de Livros Relacionados

Duas cargas puntiformes, q 1 = 2,0p C e q 2 = - 2,0p C são separadas por 4,0μ m . (a) Qual é o módulo de dipolo deste par de cargas? (b) Represente o par e mostre a direção e o sentido do momento de d
Um elétron que tem uma energia cinética igual a 2,00 × 10 - 16J está se movendo para a direita ao longo do eixo de um tubo de raios catódicos, como mostra a Figura 21-40. Um campo elétrico E → = 2,00
Um elétron é liberado a partir do repouso em um campo elétrico pouco intenso dado por E → = - 1,50 × 10 - 10N / Cy ^ . Depois que o elétron percorre uma distância vertical de 1,0μ m , qual o valor do
Qual é o campo elétrico de um núcleo de Ferro a uma distância igual a 6,00x10 - 10m do núcleo? O número atômico do ferro é igual a 26. Suponha que o núcleo possa ser considerado uma carga puntiforme.
Uma carga puntiforme de +8,75μ C está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme de -6,5μ C por um por um fio leve, não condutor, de 2,5c m . Um campo