P2 de Probabilidades da USP - 2019

Sejam e as vidas médias reais de 2 marcas concorrentes de pneus radiais. Calcule o intervalo de confiança de para considerando os seguintes dados:

10) A tabela abaixo mostra a distribuição de probabilidade conjunta de duas variáveis discretas . Não foram mostrados os valores de e mas sabe-se que as duas variáveis são independentes.

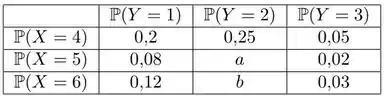
Determine .

a)

b)

c)

d)

e)

11) Sejam e duas variáveis aleatórias com valores inteiros. Sabe-se que são possíveis apenas os pares no conjunto além disso, todos os pares nesse conjunto são equiprováveis. Calcule , o valor esperado de usando a distribuição de probabilidade condicional de dado {X=1}. A resposta correta é:

A)

B)

C)

D)

E)

12) Um dado possui a seguinte propriedade: os resultados e são equiprováveis, e os resultados e também são equiprováveis; no entanto, a probabilidade de se obter um é o dobro da de se obter um . Se a variável aleatória representa o resultado de um arremesso deste dado, o valor esperado de é:

A)

B)

C)

D)

E)

13) Sabe-se que apenas dos alunos da disciplina de Probabilidade compram o livro-texto enquanto usam livros da biblioteca e/ou estudam apenas por notas de aula e materiais disponíveis no Moodle. Foram selecionados aleatoriamente alunos da disciplina. A probabilidade de que o número de alunos que compram o livro-texto dentre os selecionados seja maior que desvios-padrões acima de seu valor médio é (lembre-se: desvio padrão é a raiz quadrada da variância):

A)

B)

C)

D)

E)

14) Considere duas variáveis aleatórias e com valores esperados e e variâncias e , respectivamente. O valor de é:

A)

B)

C)

D)

E)

15) Um shopping de São Paulo possui um supermercado e uma farmácia. Sejam as variáveis aleatórias e que representam o número de vezes que um cliente assíduo desse shopping faz compras no supermercado e na farmácia durante um mês, respectivamente. A distribuição de probabilidade conjunta está na tabela abaixo. O valor médio do número de vezes que um cliente faz compra no supermercado dado que comprou vezes na farmácia vale:

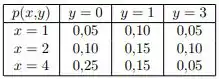
A)

B)

C)

D)

E)

03) Um plantador de cocos divide sua fazenda em lotes de para efetuar o plantio rotativo. Ele tem lotes de coco no total. Todo mês ele colhe cocos de lotes onde os cocos já estão maduros. Em dos lotes de plantas maduras, em média, ocorrem pragas e os cocos não podem ser colhidos. Qual a probabilidade de em mês não conseguir colher os cocos em apenas dos lotes?

A)

B) 2/50

C)

D)

E)

04) Cada viagem que um cobrador profissional realiza até a casa do devedor custa reais. Se encontrar o devedor em casa, evento que tem probabilidade de , o cobrador consegue receber o valor devido; os eventos relacionados a diferentes viagens são independentes. Qual é o custo médio de cobrança de um devedor?

A)

B)

C)

D)

E)

05) Uma variável aleatória contínua possui a seguinte função densidade de probabilidade:

O valor esperado de é:

A)

B)

C)

D)

E)

06) O guarda florestal Pedro sabe que em média ocorrem incêndios florestais acidentais por mês na reserva de que cuida, onde o número de incêndios em um mês segue uma distribuição de Poisson. Além disso, os incêndios em cada mês são independentes entre si. Em cinco meses de observação, qual a probabilidade de ocorrerem incêndios apenas em dos meses?

A)

B)

C)

D)

E)

07) Uma variável aleatória contínua possui a seguinte função densidade de probabilidade:

,

Para . O valor esperado de é:

A)

B)

C)

D)

E)

08) Um dado honesto é arremessado duas vezes, e define-se uma variável aleatória que representa o número de arremessos em que o resultado é igual a “1”. A variância de vale:

A)

B)

C)

D)

E)

9) Um meliante possui um conjunto grande de chaves especiais para tentar abrir uma porta de uma mansão. A probabilidade de cada chave abrir a porta é e cada tentativa leva exatamente minutos. Uma viatura passará em exatamente minutos após o meliante começar suas tentativas e o prenderá com certeza se o meliante estiver fora da casa, mas com probabilidade se este estiver dentro da casa. Qual é o valor mais próximo da probabilidade do meliante ser preso?

a)

b)

c)

d)

e)