P3 de Probabilidades da USP - 2018

Experimentos com animais indicam que o tempo necessário para que um determinado remédio contra febre faça efeito segue uma distribuição uniforme no intervalo 20 a 50 (em minutos). Qual a probabilidade da febre de uma pessoa que tomou esse remédio durar mais de 40 minutos, sabendo-se que sua febre não cedeu 30 primeiro primeiros minutos após ter tomado o remédio?

Seja uma variável aleatória discreta distribuida conforme a distribuição de Poisson. Seja a variável aleatória binomial usada na "aproximação da Poisson pela Binomial". Nesse contexto, considere as seguintes afirmações.

a) .

b)

c) .

Quais alternativas são corretas?

11) Considere as afirmações a respeito de uma variável aleatória discreta que assume apenas valores reais.

(a) (b) (c)

Quais alternativas são corretas?

a) Só (a).

b) Só (a) e (c).

c) Só (a) e (b).

d) Só (b) e (c).

e) Só (c).

13) Dimensione o comprimento médio de uma prateleira para acomodar latas quadradas de tinta que tem larguras normais de valor esperado e desvio padrão . Deseja-se que as latas escolhidas aleatoriamente (de forma independente) caibam na prateleira e que a probabilidade de deixarem uma folga menor que entre a última lata e o final da prateleira seja menor que . Admita que as latas foram encostadas à esquerda no início da prateleira.

a)

b) 0

c)

d)

e)

Obtenha , se a função de densidade de probabilidade conjunta das variáveis aleatórias é:

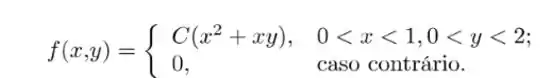
Considere duas variáveis aleatórias contínuas e independentes ambas com distribuição exponencial com e . Qual a probabilidade de ?

O tempo de vida de uma máquina é uma variável aleatória contínua , expressa em anos. Sabe-se que , sendo uma constante. Considere uma máquina que está em operação a um ano. Qual a probabilidade dessa máquina funcionar por mais dois anos.

A função de densidade de probabilidade conjunta para duas variáveis aleatórias para uma constante é dada por:

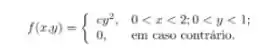
A densidade marginal de para

Um sistema é constituído de componentes que funcionam de forma independente. Sabe-se que se um dos componentes falhar o sistema falha. O tempo de vida de cada um dos componentes segue uma distribuição exponencial cujos valores esperados são: , e . Qual a probabilidade de o sistema não falhar antes de ?

A função de densidade de probabilidade conjunta de duas variáveis aleatórias é dada por:

A densidade condicional de dado para é:

O preço da gasolina aditivada () no Brasil depende do valor do preço da gasolina comum (), do etanol () e dos aditivos (), seguindo a função . Sabe-se que os preços por litro dos componentes da gasolina aditivada podem ser modelados por variáveis aleatórias independentes com distribuições normais com médias e variâncias mostradas na tabela abaixo.

A probabilidade que o preço da gasolina aditivada ultrapasse R$7,00 o litro é aproximadamente:

12) O tempo que um aparelho eletrônico funciona sem apresentar defeito tem distribuição exponencial com média . Este não apresentou defeito até o momento, mas não se sabe por quanto tempo já foi usado. Qual a probabilidade de que não apresente defeito durante as próximas ?

a) .

b) é necessário saber .

c) .

d) .

e) .

14) A variável aleatória é obtida a partir da soma de variáveis aleatórias independentes, todas com distribuição uniforme em (ou seja, . Y=Uma aproximação para a função densidade de probabilidade de é mostrada na figura ao lado. Os valores de e são respectivamente iguais a:

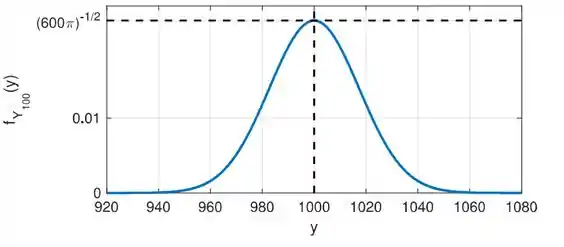
a) e

b) e

c) e

d) e

e) e

15) Um comprimido é produzido em série numa empresa farmacêutica com peso médio de e desvio padrão de com distribuição normal. Os comprimidos passam por um controle de qualidade e os comprimidos com peso menor que e peso maior que são eliminados do lote. Qual a probabilidade de nesse lote restante retirarmos ao acaso um comprimido com peso entre os valores e ?

a)

b)

c)

d)

e)