P2 de Probabilidades da USP - 2018

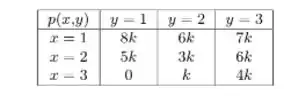
Sejam as variáveis aleatórias e , que representam o número de vezes que um ingressante de 2014 cursou a disciplina Cálculo I e a disciplina Probabilidade, respectivamente. A distribuição de probabilidade conjunta está na tabela abaixo. O valor médio do número de vezes que o ingressante de 2014 cursou a disciplina Probabilidade dado que cursou Cálculo I uma única vez vale:

Seja , uma sequência de variáveis aleatórias independentes (resultados de 3 experimentos idênticos mas independentes). Sabe-se que

Deseja-se estimar μ com o seguinte estimador: μb = (X1 + X2 + X3)/3.

A variância de μb é igual a:

Considere um experimento em que um número real R é sorteado do intervalo Ω = [0,1]. A probabilidade do número sorteado cair em um intervalo de comprimento L é L. Sejam os intervalos = [0,a] (a ∈ Ω) e = [ 1/8, 5/8]. Definem-se as variáveis aleatórias: = 1 se R ∈ , = 0 caso contrário, e analogamente = 1 se R ∈ , = 0 caso contrário.

Dentre as afirmações a seguir, quais são verdadeiras?

a) Pode-se afirmar que ∃a ∈ Ω tal que os eventos e são independentes.

b) Pode-se afirmar que ∃a ∈ Ω tal que as variáveis aleatórias e são independentes.

c) A correlação entre e é sempre nula, qualquer que seja a ∈ Ω.

Considere duas variáveis aleatórias X e Y , independentes, e ambas com distribuição geométrica com parâmetro p. O valor de P (X = Y ) é:

Sejam X e Y duas variáveis aleatórias. Dentre as afirmações a seguir, quais são verdadeiras?

a) Se X e Y são independentes: E[XZ] = Cov[X,Y + Z] + E[X].E[Z] , para qualquer variável aleatória Z

b) Cov[X + Y, X − Y ] = V [X] − V [Y ] + 2Cov[X,Y ]

C) Cov[X + Y, X + Y ] = V [X] + V [Y ] + 2Cov[X,Y]

Numa fábrica de artefatos de porcelana, situada em São Paulo, o processo consiste de duas fases: cozimento e pintura. Na primeira fase, a probabilidade de ocorrência de falhas é de . Na segunda fase, os defeitos ocorrem segundo uma distribuição de Poisson, com parâmetro falhas peças se ocorreu falha na fase de cozimento e com parametro falhas/ peças caso contrário. Se ocorrer defeito em nenhuma ou em apenas uma das fases o produto é vendido por à unidade. Se ocorreu defeito nas duas fases o preço passa a . Qual o valor médio de venda de uma peça?

Para X e Y duas variáveis aleatórias discretas, que possuem distribuição conjunta de acordo com a tabela abaixo, quais são os valores de ?

A função distribuição cumulativa de uma variável aleatória é definida da seguinte forma: igual a para , para, para, para .

Dentre as afirmações a seguir, quais são verdadeiras?

1. e ;
2. , sendo constantes;
3. e .

1. Só (c)
2. Só (b)
3. Só (b) e (c)
4. Só (a) e (c)
5. Só (a)

Considere duas variáveis aleatórias e , independentes, e ambas com distribuição geométrica com parâmetro . Considere também duas variáveis e. O valor de é:

Um lote de sinalizadores navais está sendo testado antes de ser entregue a uma guarnição do Corpo de Bombeiros. O ensaio consiste em acender o sinalizador e verificar o tempo de queima. O engenheiro deseja lotes sem nenhuma sinalizador defeituoso. Imaginou um ensaio que consiste em retirar do lote sinalizador e testá-lo; se o sinalizador não falhar o lote é aceito; caso contrário o lote é rejeitado. No teste de lotes idênticos, cada um com sinalizador não conforme, qual a probabilidade de serem aceitos mais de desses lotes com problemas?

Uma urna contém bolas numeradas e . Duas bolas são retiradas sucessivamente da urna, ao acaso e sem reposição. Seja o número da primeira bola tirada e o número da segunda bola. O valor de é:

Uma moeda honesta é jogada repetidamente. Qual a probabilidade de se obter caras antes de aparecerem coroas?

A probabilidade de um atirador acertar o alvo em um único tiro é . Quantas vezes ele deve atirar de modo que a probabilidade dele acertar o alvo pelo menos uma vez seja maior que ?

3. Nunca fia maior que

A tabela abaixo mostra a distribuição de probabilidade conjunta das variáveis aleatórias e .

Sabe-se que . Dentre as afirmações a seguir, quais são verdadeiras?

a) e são variáveis independentes e .

b) e .

c) e.

1. Só (a)
2. Só (c)
3. Só (a) e (b)
4. Só (b)
5. Só (b) e (c)

O setor de manutenção de uma empresa consegue atender até 2 casos de quebra de impressoras em um dia ou horas extras serão necessárias naquele dia. A média de quebras é de 2.0 impressoras por dia; a distribuição do número de quebras é Poisson. Qual é a probabilidade de serem necessárias horas extras pelo menos em algum dia da semana de trabalho (5 dias)?