8) Efetue as divisões de polinômios (encontrando o quociente e resto) e escreva as duas identidades associadas à divisão, conforme exemplo no item (a);
a)
Quociente: ; Resto: 19;
Identidade (forma 1):
Identidade (forma 2):
b)
c)
d)
e)
f)
Passo 1
Falaaaa... tudo bem??
Nessa questão vamos efetuar as divisões dos polinômios e escrever conforme os exemplos.
Vamos tentar entender como o exemplo foi feito passo a passo.
Se a gente montar uma conta de divisão mesmo com os polinômios:

Temos o numerados na esquerda e o denominador na direita, certo?
O que a gente precisa multiplicar o da direita pra ele ficar igual ao da esquerda?? , certo??
A gente o escreve embaixo, à direita.
Agora multiplicar e o resultado colocamos lá embaixo do numerador (esquerda), maaas com o sinal de menos:
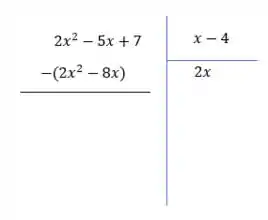
Fazemos a conta e depois repetimos até o final, que é quando não der pra multiplicar por mais nada:
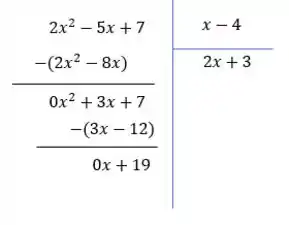
Daí ficamos com:
Identidade (forma 1):
Identidade (forma 2):
Passo 2
b)
Fazendo o algoritmo:

Identidade (forma 1):
Identidade (forma 2):
Passo 3
c)
Fazendo o algoritmo:
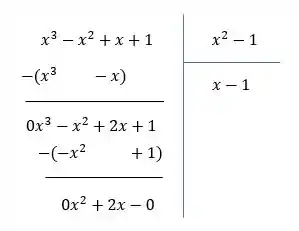
Identidade (forma 1):
Identidade (forma 2):
Passo 4
d)
Aqui temos um caso diferente.
Repara que o maior expoente do polinômio que está dividindo é maior que o maior expoente do outro polinômio. Então não dá pra fazer a divisão mesmo...
Passo 5
e)
Fazendo o algoritmo:
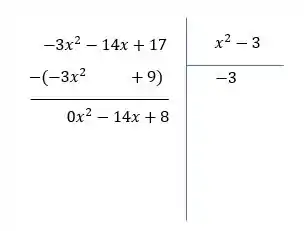
Identidade (forma 1):
Identidade (forma 2):
Passo 6
f)
Fazendo o algorítmo:

Identidade (forma 1):
Identidade (forma 2):
Resposta
Respostas nos passos