UFSC. Exame de Proficiência. Pré-Cálculo. Calculo. 2018.1. Questão 10.
Questão 10. O resto da divisão de por é
A) ; B) ; C) ; D) ; E) .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão, temos que calcular a divisão do polinômio por
Minha nossa!! Divisão de polinômios!! Mal sei dividir números inteiros 🤦♂️
Relaxa, as propriedades que usamos para dividir um número inteiro vão ser as mesmas pra a divisão de polinômios.
A questão quer saber qual será o resto da divisão dos polinômios que indicamos acima. Lembra o que é esse valor em uma divisão?
Veja só.
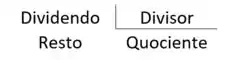
Depois de fazermos toda a divisão, vamos chegar em um valor que não será mais possível dividir, esse valor será nosso resto.
Entendeu? Bora para os cálculos.
Passo 2
Vamos calcular a seguinte divisão
Para cada passo, a pergunta que devemos fazer é: “qual valor eu multiplico o primeiro termo do divisor para ser igual ao primeiro termo do dividendo?”
Ou seja, multiplicamos por quanto pra ele ficar igual a ?
Bem, se multiplicarmos por , vira
Porém, não multiplica apenas , ele multiplica o divisor todo, então
Esse valor entra com o sinal trocado, então fazemos a subtração de com , resultando em
Entendeu como funciona?
Passo 3
Agora fazemos a mesma pergunta novamente.
Devemos multiplicar pelo que para ficar igual a . Vemos que se multiplicarmos por , temos
Trocando o sinal, temos
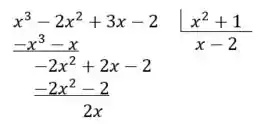
Chegamos no fim, já que o grau do resto é menor que o grau do divisor!
Analisando a divisão que fizemos, percebemos que o resto da divisão foi
Ou seja, a letra D) de “doidão”
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
D) .