9) Existe uma forma “prática” para calcular a divisão entre polinômios no caso em que o divisor é da forma , em que é um número. Este processo se chama Algoritmo de Briot-Ruffini (ou Dispositivo de Briot-Ruffini). Pesquise sobre esse processo e utilize-o para efetuar as divisões abaixo:

a)

b)

c)

a)

Primeira coisa que fazemos é traçar tipo uma estrutura de divisão:

Na parte isoladinha, na esquerda, colocamos o valor que zera o numerador da divisão:

E na parte superior da direta colocamos só os coeficientes do polinômio que está no numerador. (importante não esquecer dos zeros, heim?? Repara que não termos um termo de , então representamos ele como )

Ficamos assim:

Repita o primeiro número que aparece na parte de cima à direita:

Multiplique esse número pelo que está isoladinho à esquerda e some com o próximo número:

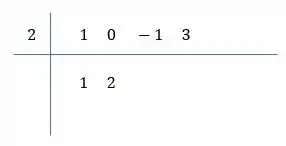
Pega o resultado, multiplicar pelo isoladinho e soma com o próximo:

E faça isso até o final.

E pra montar o resultado separamos o último número da linha que montamos, ele vai ser o resto da divisão.

Os outros números são os coeficientes do polinômio que achamos.

b) )

Montando o algoritmo:

E ficamos com:

c)

Montando o algoritmo:

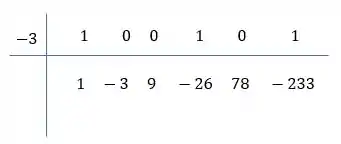
E ficamos com: