O perímetro de um triângulo retângulo é e a hipotenusa é . Exprima a área do triângulo como função de .
Passo 1
Olááá, meu anjo! Como eu te disse na teoria, é muito comum, em polinômios, aparecer questões de modelagem de área ou volume, etc.
Primeiramente, vamos desenhar o que temos até agora:
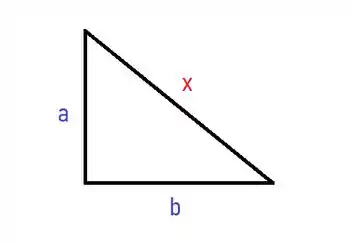
Esse é o desenho! Agora vamos escrever matematicamente o que ele diz em “o perímetro é ”:
E quando ele diz que é um triângulo retângulo, podemos assumir:
Passo 2
Maneiro, e o que queremos é:
Vamos ter que manipular as duas equações que temos para obter esse produto em função de .
Passo 3
Comecemos com a seguinte equação:
Bom, a gente sabe que na outra equação temos um , e a única forma desses termos aparecerem é se fizermos as seguintes manipulações:
E olha só o que apareceu!!!
Eu não expandi o lado direito da igualdade por não haver nada que vá nos ajudar!
Passo 4
Agora, da outra equação temos:
Então podemos substituir essa relação nesta equação:
Substituindo:
OPAAAAAA, encontramos em função de !!! Ainda não viu? Saca só:
Ao simplificarmos os termos, ficamos com:
Dividindo todo mundo por 2, ficamos assim:
Passo 5
Finalmente, substituindo onde queríamos desde o início: