Um banhista olha para dentro de uma piscina em uma parte com profundidade real de . O índice de refração da água da piscina é aproximado por .
Utilizando a aproximação de pequenos ângulos para os feixes incidente e refratado, estime a profundidade aparente da piscina observada pelo banhista.
Passo 1
A relação entre a profundidade real e a profundidade aparente é dada aproximadamente por:
Se tivermos essa fórmula na mão, é só substituir!
Que é a letra .
Mas... que droga de fórmula é essa e daonde ela surgiu???
Vamos mostrar nos passos 2 e 3.
Passo 2
Vamos começar fazendo uma análise gráfica do problema, mas para isso teremos que definir algumas coisas. Imagine dois raios, cada um saindo do fundo da piscina e indo pra cada olho do banhista.
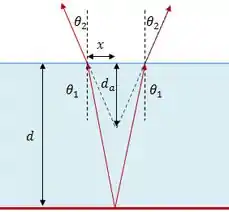
Na figura acima, e são os ângulos formados com a normal pelos raios incidentes e refratados, respectivamente. Além disso, é a distância entre o ponto em que os raios cruzam a interface entre os dois meios e o eixo central do ponto que definimos.
Daqui podemos separar dois triângulos:
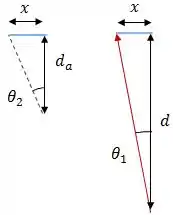
As tangentes de e são, respectivamente:
Considerando e suficientemente pequenos (aqui está aproximação do enunciado), podemos dizer que:
Passo 3
De acordo com a Lei de Snell, temos que:
Onde e, de acordo com o enunciado, , logo:
Fazendo as substituições das expressões que encontramos no Passo 2, teremos:
Organizando os termos, teremos, finalmente:
Uma observação: Não faz muita diferença se você considerar dois raios, um pra cada olho do banhista, ou pensar um banhista pontual olhando a quina da piscina.
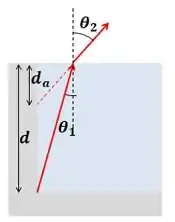
Porque acabaríamos usando os mesmos dois triângulos retângulos. A ideia de “dois raios, um pra cada olho” é só pra garantirmos que tem dois raios formando a imagem do chão da piscina ou de qualquer objeto no chão da piscina.
Mas as duas imagens estão conceitualmente corretas.
Resposta
Letra