A figura abaixo ilustra um raio policromático incidindo na superfície de um paralelepípedo (a reta normal á superfície de incidência está indicada na figura).
O índice de refração do ar é e o índice de refração do paralelepípedo é função da frequência, maior que para toda frequência e satisfaz .
Sendo as frequências dos raios , respectivamente, podemos afirmar que
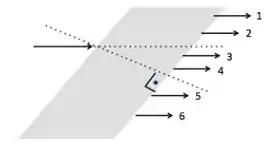
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
Passo 1
Vamos um passo de cada vez.
De acordo com o enunciado, o índice de refração do paralelepípedo é maior que , o índice de refração do ar.
Assim, o raio de luz vai sofrer um desvio de forma a se aproximar da normal. Além disso, como ele passa pelo paralelepípedo e depois volta para o ar, o raio que saio vai ser paralelo ao que entra.
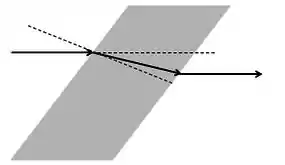
(Essa última talvez não seja tão fácil ver, mas a idéia é que a reta normal na saída é paralela à da entrada, e por isso o ângulo de refração na entrada é igual ao ângulo de incidência na saída.)
Uma terceira observação: Em refração, não existe raio de luz desviando tanto que ele atravessa a reta normal à interface.
Logo, os únicos raios realmente possíveis de vermos nesse experimento são os raios e . Os raios são impossíveis.
Isso já reduz nossas opções para as letras e .
Passo 2
De acordo com o enunciado, o índice de refração do paralelepípedo varia com as frequências de forma que
Isso significa que o índice de refração é crescente com a frequência. Além disso, quanto maior o índice de refração, mais o raio refratado se aproxima da normal, e o raio que sai vai mais pra baixo.
Como o raio desceu mais, ele se aproximou mais da normal, o que significa que e, logo, .
A resposta então é a letra .
Resposta
Letra
e os raios , , e não existem.