Uma onda eletromagnética plana e monocromática propaga-se num meio material com permeabilidade magnética igual a .
No instante , os campos elétrico e magnético são descritos por e , onde e são funções de apresentadas na figura abaixo.
São dados:
e
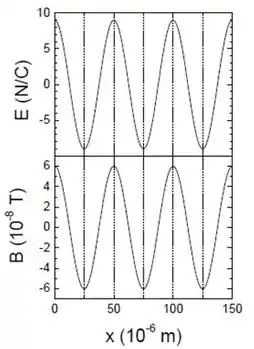
- Qual é a direção de propagação dessa onda? Justifique.
- Quais são a velocidade dessa onda e o índice de refração do meio?
- Qual é o valor da permissividade desse meio?
- Qual é a frequência dessa onda?
- Em relação a esta onda, qual é a média temporal da energia contida num volume correspondente a um metro cúbico?
Passo 1
Letra a)
Primeiro, para sabermos a direção da propagação de onda, podemos usar a direção de vibração dos campos elétrico e magnético.
A onda eletromagnética se propaga no mesmo sentido que o produto vetorial entre os campos:
Onde é o vetor unitário na direção do eixo e é o vetor unitário na direção do eixo . Usando a regra da mão direita, podemos colocar nossa mão direita no sentido de , com a palma voltada para e avaliar o sentido do produto vetorial como sendo o do nosso dedão.
Logo:
Onde é o vetor unitário no sentido do eixo . A onda se propaga então no sentido negativo do eixo .
O produto não altera esse resultado pois e têm o mesmo sinal, pois pelos gráficos quando temos e quando temos , o que implica que .
Passo 2
Letra b)
A velocidade da luz é dada pela relação:
Independente do ponto do eixo que usarmos para calculá-la, o valor dará sempre o mesmo. Sendo assim, usando e os gráficos acima, temos:
Passo 3
Agora, vamos encontrar o índice de refração do meio.
Ele é a razão entre a velocidade da luz no vácuo e a velocidade da luz no meio.
Passo 4
Letra c)
Podemos relacionar a velocidade da luz em um meio com a permissividade elétrica e a permeabilidade magnética do meio. Essa relação é:
Onde é a permissividade elétrica do meio e é a permeabilidade magnética do meio. Pelo enunciado a permeabilidade magnética é a mesma que no vácuo:
E rearrumando a equação acima:
Substituindo na equação da refração, lembrando que é a velocidade da luz no vácuo (logo, usamos a permissividade e a permeabilidade do vácuo):
Elevando ao quadrado:
Dos itens anteriores e do enunciado:
Passo 5
Letra d)
Os gráficos da questão nos dizem o valor dos campos elétrico e magnético ao longo do eixo . Isso nos permite encontrar o comprimento da onda vendo a distância entre duas cristas.
A velocidade de uma onda é dada por:
Podemos então usar a velocidade obtida nos itens anteriores, junto com o comprimento de onda e calcular a frequência:
Passo 6
Letra e)
A densidade de energia de uma onda eletromagnética cujo campo elétrico tem amplitude é dada por:
O valor médio da densidade de energia é:
Pelo gráfico, vemos que oscila de forma bem parecida com um seno ou coseno e, sendo assim, oscila como seno ou coseno ao quadrado.
Mas a média de uma função seno ao quadrado é igual a média dos valores entre os quais ela oscila. Como oscila entre e , logo sua média fica em . Substituindo:
Do gráfico e dos itens anteriores:
Como temos , a energia média nesse volume será:
Resposta
Letra a)
A onda se propaga no sentido negativo do eixo .
Letra b)
Letra c)
Letra d)
Letra e)