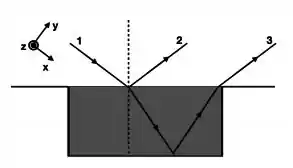
Enunciado Um feixe de luz monocromática, bem colimado e de pequeno diâmetro, propaga-se no ar e atinge a interface de uma piscina com água (n = 1,33), de profundidade 1,6m. Considere que esse feixe é emitido a partir de uma altura de 40 cm em relação à superfície da água, fazendo um ângulo de 45° com a normal à superfície.
(a) Parte do feixe penetra na água, reflete no fundo da piscina e volta ao ar (ver figura).
Qual é o caminho ótico percorrido por este feixe entre os pontos 1 e 3, estando o
ponto 3 à mesma altura do ponto 1?
Passo 1
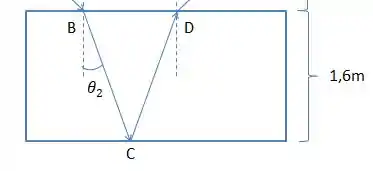
Nessa questão o enfoque principal é que calculemos o caminho óptico, sabemos que para calcularmos o caminho óptico de um feixe de luz devemos pegar o caminho total que aquela luz percorreu em determinado meio e multiplicar pelo índice de refração do meio em que ela percorreu, se analisarmos a figura teremos.
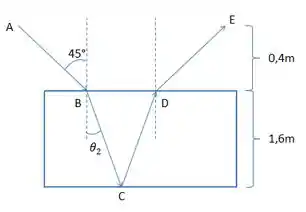
Sabemos que e que
Vamos agora determinar o tamanho dos trechos
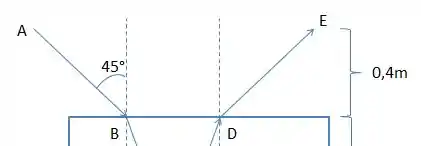
Pela lei de Snell sabemos que o ângulo de saída em D também deve ser igual ao de entrada, ou seja 45°, logo
Passo 2
Agora para determinar precisamos do ângulo dentro da água que determinamos facilmente pela lei de Snell.
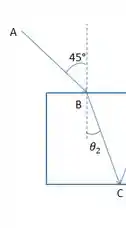
E já sabemos que o trecho BC=CD, então,
Passo 3
Agora que já sabemos todos os valores de distancia basta substituir na fórmula de caminho óptico
Logo o caminho óptico será
Resposta
a)