Uma pessoa enxerga uma lâmpada no fundo de uma piscina através de raios luminoso próximos da normal. Ele estima a profundidade da piscina em . Do lado da piscina, existe um alerta para crianças, indicando a profundidade real de .
A discrepância entre a estimativa da pessoa e o valor correto é devido à profundidade aparente ocasionada pela refração da luz.
Utilizando a aproximação de pequenos ângulos para os ângulos dos feixes incidente e refratado, determine o índice de refração do líquido da piscina.
- 1,4
- 1,6
- 1,8
- 2,0
- 2,2
Passo 1
Nessa questão, vamos precisar de algumas sacadas para enxergar a fórmula final que procuramos. Ela vai ser a seguinte:
Onde é a profundidade aparente da piscina, é a profundidade real da piscina e é o índice de refração da água.
De posse dessa fórmula, o final vai ser rápido:
Então se seu professor deu essa equação, esse problema se resolve em um passo. Caso contrário, me siga aqui nos próximos passos.
Passo 2
Para a formação da imagem que vemos, são necessários dois raios de luz se cruzando, um no nosso olho direito e outro no nosso olho esquerdo.
Como a pessoa está olhando raios bem próximos da normal, podemos imaginar a situação assim.
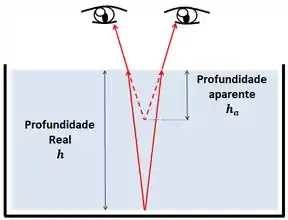
Com a figura do que está rolando, podemos então resolver a geometria.
Passo 3
Vamos observar como ficou a geometria do problema, tirando esses olhos sedutores.
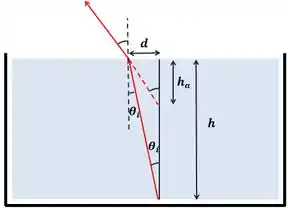
Pela figura, a normal à superfície da piscina é paralela à altura.
Por isso, o ângulo que o raio faz com a altura é igual ao ângulo incidente quando o raio sai da piscina.
Pela mesma razão, podemos passar o ângulo refratado pro ponto onde o prolongamento do raio bate com a altura.
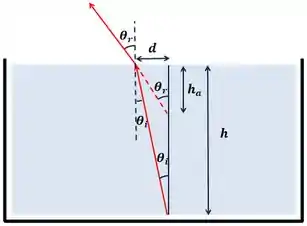
O que nos dá dois triângulos retângulos, um com catetos e e outro com catetos e .
Passo 4
De cada triângulo, temos:
Ok, ainda não chegamos a lugar nenhum assim. Mas a gente pode relacionar os dois ângulos pela lei de Snell, e sumir com eles.
Por fim, senhoras e senhores, vem o milagre que todos esperávamos: APROXIMAÇÃO DE PEQUENOS ÂNGULOS!!!! (“barulho de palmas”).
Substituindo:
Que é aquela nossa equação lá do primeiro passo!
Quando substituímos:
A resposta é a letra (d).
Resposta
Letra (d)