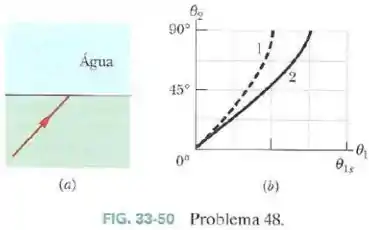
Na Fig.33-50a um raio luminoso que está se propagando inicialmente em um certo material incide com um ângulo na água, onde parte da luz se refrata. O outro material pode ser do tipo ou do tipo ; a FIg.33-50b mostra o ângulo de refração em função do ângulo de incidência para os dois tipos de material.
A escala do eixo horizontal é definida por . Sem fazer nenhum cálculo, determine:
- Se o índice de refração do material é maior ou menor que o índice de refração da água ().
- Se o índice de refração do material é maior ou menor que o índice de refração da água.
- Do material .
- Do material .
Determine o índice de refração:
Passo 1
Letra a)
Seja o índice de refração da água e o índice de refração do material.
- O ângulo de refração é menor que o ângulo de incidência somente se .
- O ângulo de refração é maior que o ângulo de incidência somente se .
Lembrando que a luz está refratando na água.
Como o ângulo de refração é sempre maior que o ângulo de incidência para a curva 1:
Passo 2
Letra b)
Semelhante ao caso da letra , o ângulo de refração da curva é sempre maior que o ângulo de incidência. Isso nos diz que:
Passo 3
Letra c)
A unidade do eixo horizontal do gráfico é de , ou seja, .
Assim, olhando a curva para , teremos
Passo 4
Letra d)
Olhando a curva , para teremos .
Resposta
Letra a)
Letra b)
Letra c)
Letra d)