Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei da Refração

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930

Enunciado

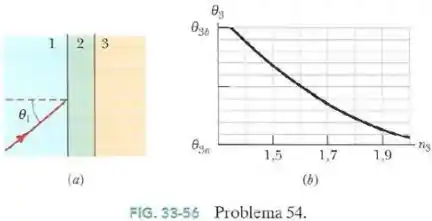
Na Fig.33-56a um feixe de luz que estava se propagando no material 1 incide com um ângulo θ 1 = 40 ° na interface com o material 2 . Parte da luz penetra no material 2 e parte dessa luz penetra no material 3 ; todas as interfaces são paralelas.

A orientação do feixe no material 3 depende em parte do índice de refração n 3 do terceiro material. A Fig.33-56b mostra o ângulo θ 3 em função de n 3 .

A escala do eixo vertical é definida por θ 3 a = 30,0 ° e θ 3 b = 50,0 ° .

  1. É possível calcular o índice de refração do material 1 com base nessas informações? Se a resposta for afirmativa, determine o valor de n 1 .
  2. É possível calcular o índice de refração do material 2 com base nessas informações? Se a resposta for afirmativa, determine o valor de n 2 .
  3. Se θ 1 = 70 ° e n 3 = 2,4 , qual é o valor de θ 3 ?

Passo 1

Letra a)

Vamos aos poucos, evitando terrenos perigosos.

O ângulo de refração da luz incidente na interface material 1 -material 2 é dado por:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

sen ⁡ θ 2 = n 1 sen ⁡ θ 1 n 2

Porém, pelo fato das interfaces serem paralelas, às retas normais à elas também vão ser paralelas, e o ângulo de refração θ 2 vai ser o ângulo de incidência na interface material 2 -material 3 .

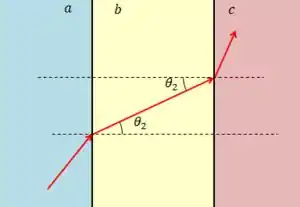
Aplicando a lei de Snell nessa interface:

n 2 sen ⁡ θ 2 = n 3 sen ⁡ θ 3

n 2 ∙ n 1 sen ⁡ θ 1 n 2 = n 3 sen ⁡ θ 3

n 1 sen ⁡ θ 1 = n 3 sen ⁡ θ 3

Como temos θ 1 = 40 ° e ambos θ 3 e n 3 podem ser obtidos pelo gráfico, é possível encontrar n 1 .

Passo 2

O ideal é acharmos o ponto correspondente a θ 3 = 40 ° no gráfico.

Esse ângulo corresponde à metade do eixo vertical (que varia de 30 ° a 50 ° ) e ele corresponde, no eixo horizontal, ao ponto médio entre os índices de refração 1,5 e 1,7 , significando que o índice correspondente é n 3 = 1,6 .

n 1 sen ⁡ θ 1 = n 3 sen ⁡ θ 3

n 1 sen ⁡ 40 ° = 1,6 ∙ sen ⁡ 40 °

n 1 = 1,6

Passo 3

Letra b)

Poderíamos tentar usar duas fórmulas para calcular n 2 . A primeira é:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Mas neste caso, temos n 1 (pela letra a ) e θ 1 (pelo enunciado), mas não temos θ 2 , o que nos impossibilita de achar n 2 .

A outra fórmula seria:

n 2 sen ⁡ θ 2 = n 3 sen ⁡ θ 3

Mas nós cairíamos no mesmo problema! Temos vários valores possíveis de n 3 e θ 3 , mas sem θ 2 não temos como encontrar n 2 .

Nós poderíamos tentar usar uma das duas equações para achar θ 2 e a outra para n 2 . Cairíamos no conto do vigário:

Pra achar θ 2 precisaríamos de n 2 e pra achar n 2 precisaríamos de θ 2 !

É um raciocínio circular. Então não temos como encontrar n 2 .

Passo 4

Letra c)

Vimos na letra a que vale:

n 1 sen ⁡ θ 1 = n 3 sen ⁡ θ 3

Substituindo n 1 = 1,6 , θ 1 = 70 ° e n 3 = 2,4 :

sen ⁡ θ 3 = n 1 sen ⁡ θ 1 n 3 = 1,6 ∙ sen ⁡ 70 ° 2,4 ≅ 0,626

θ 3 ≅ sen - 1 ⁡ 0,626 ≅ 38,79 °

Resposta

Letra a)

É possível calcular n 1 .

n 1 = 1,6

Letra b)

Não é possível calcular n 2 .

Letra c)

θ 3 ≅ 38,79 °

Exercícios de Livros Relacionados

Uma esfera transparente de índice de refração n , espelhada numa calota A B da sua superfície, com centro em C (fig.), é usada como retro-refletor: qualquer raio 1 paralelo ao eixo C D e paraxial (pró
O índice de refração de um meio inomogêneo, em função da altitude z , é dado por n = n 0 + n ' z , onde n 0 e n ' são constantes. Um raio luminoso no plano ( x z ) parte da origem numa direção de cose
Um raio de luz no ar incide na superfície de um pedaço de vidro. O ângulo entre a normal à superficie e o raio incidente é 40°, e o ângulo entre a normal e o raio refratado é 28°. Qual é o ângulo entr
• O material A tem um índice de refração maior que o material B. Qual material tem um ångulo crítico maior para a reflexão interna total quando estiver no ar? (a) A, (b) B, (c) os angulos são iguais.