Na Fig.33-53 uma estaca vertical com de comprimento se projeta do fundo de uma piscina até um ponto acima da água. O sol está acima do horizonte.
Qual é o comprimento da sombra da estaca no fundo da piscina?
O índice de refração da água é de .

Passo 1
Primeiro, o ideal é tentarmos montar a geometria do problema, para não nos perdermos no nosso objetivo.
A sombra da estaca vai ser projetada por um raio que passa no topo dela, bate na superfície da água e, por causa da Lei de Snell, tem sua direção alterada ao entrar na água, e forma uma sombra no fundo da piscina.
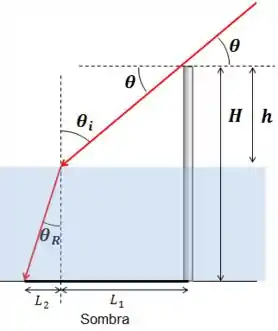
Passo 2
Agora que já montamos o problema em um desenho (bem bonito, por sinal, e fui eu que fiz =D ) podemos tentar ver o comprimento da sombra.
Vamos de trás pra frente:
Podemos pensar na sombra em duas partes.
Uma parte vai da base da estaca até o comprimento que a luz entra na água. Ela é dada por:
A segunda parte vai ser:
Então, precisamos encontrar os ângulos de incidência e refratado.
Passo 3
Para o ângulo de incidência, note que temos um triângulo retângulo com os ângulos internos e e o enunciado nos diz que . Isso significa que:
Já para o ângulo refratado nós podemos usar a lei de Snell:
Lembrando que o índice do ar é aproximadamente , e o problema nos diz que :
Lembrando que se você precisar transformar ângulos de grau pra radiano e vice versa (caso sua calculadora só tenha um ou outro) você pode usar a regra de três:
Passo 4
Finalmente temos todas as informações necessárias para encontrar o comprimento da sombra.
- Pelo passo anterior, e .
- Pelo enunciado, e .
Logo, além do meu desenho estar extremamente fora de escala, o comprimento da sombra é:
Resposta
O comprimento da sombra é de .