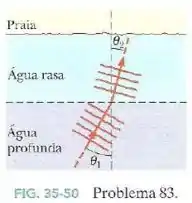
Ondas oceânicas, com uma velocidade de , se aproximam da praia fazendo um ângulo de com a normal, como se vê na vista de topo da Fig.35-50. A profundidade da água muda bruscamente a uma certa distância da praia, fazendo a velocidade das ondas diminuir para .
- Qual é o ângulo entre a direção das ondas e a normal perto da praia? (Suponha que a lei de refração é a mesma que para a luz)
- Explique por que quase sempre as ondas incidem perpendicularmente à praia, mesmo quando se aproximam da costa fazendo um ângulo relativamente grande com a normal.
Passo 1
Letra a)
No caso da água, nós não podemos simplesmente definir um “índice de refração” como a razão da velocidade da luz no vácuo e a velocidade de uma onda de água na água salgada. Isso não faria nenhum sentido! (isso não te impediria de tentar definir mesmo assim, e fazer dar certo, porque daria certo mesmo)
Mas vamos olhar a lei de refração de uma forma um pouco diferente, abrindo a definição do índice de refração:
Ela vai ficar:
Onde cortamos a velocidade da luz no vácuo de um lado e do outro. Dessa forma faz mais sentido sairmos colocando valores para ondas de água invés de ondas eletromagnéticas né?
Passo 2
A onda incidente faz um ângulo e tem uma velocidade de enquanto a onda refratada tem uma velocidade de .
Assim, rearranjando a equação anterior:
Passo 3
Letra b)
O ângulo que a onda da letra (a) faz com a praia é:
Que é “quase perpendicular” (ok, forcei um pouco a barra).
Se olharmos a equação que nos dá o ângulo da onda refratada, e considerarmos que as ondas sempre perdem velocidade ao chegar perto da praia, vemos que:
Ou seja, a onda sempre se aproxima da normal à praia quando ela vai perdendo velocidade devido à profundidade da água.
Se, desde o ponto que ela se forma, até a praia, ela perder a velocidade diversas vezes, o ângulo que ela faz com a normal vai diminuir cada vez mais, até que seja praticamente igual a zero.
Resposta
Letra a)
Letra b)
Quase sempre as ondas incidem perpendicularmente à praia pois a medida que elas vão perdendo velocidade, seu ângulo com a direção normal à praia vai diminuindo até que seja quase igual a zero.