Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Medidas de Centralidade e Dispersão para V.A. Contínua

Ver Teoria
Exercício 1234567891011121314151617181920212223

Enunciado

Calcule a esperança, a variância e a f.d.a. da variável aleatória X com a densidade triangular em 0 ,   1 .

Passo 1

Primeiro temos que entender como é a função triangular de 0 a 1 :

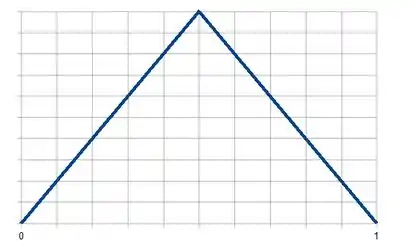
E pra valores fora desse intervalo, nossa função vale zero. E podemos considerar que esse aí é um triângulo isósceles, então o ponto médio da nossa função é na metade do intervalo, ou seja, 0,5 . E repara comigo, até 0,5 temos uma reta crescente, e depois desse ponto temos outra reta, agora decrescente. Temos que descrever essas duas retas como funções.

Passo 2

A gente sabe que a área de um triângulo é dada por B h 2 , certo? E como esse triângulo é uma função de densidade, vamos igualar essa área a 1 para descobrir o valor de h (o ponto máximo dessa função). Estamos fazendo isso porque a área nada mais é que uma integral! Então:

B h 2 = 1

Mas sabemos que a base é nosso intervalo [ 0,1 ] :

1 × h 2 = 1 → h = 2

Então o ponto máximo da nossa função é 2 . Agora podemos descobrir as equações para as nossas duas retas. Vamos começar pela crescente.

Ela corta o gráfico no ponto ( 0,0 ) e 1 2 , 2 , e como é uma reta, vai ter formato f ( x ) = a x + b . Substituindo os pontos conhecidos obtemos o sistema:

0 = a 0 + b 2 = a 1 2 + b

Disso aí descobrimos que b = 0 e a = 4 . Então nossa equação fica f x = 4 x

Agora vamos ver a segunda reta. Ela tem os pontos 1 2 , 2 e 1,0 . Temos então o sistema:

2 = a 1 2 + b 0 = a + b

Isso dá pra gente que a = - 4 e b = 4 . Então f x = - 4 x + 4 = 4 ( - x + 1 ) .

Juntando as duas retas, nossa função de densidade é dada por:

f x = 4 x   ,     s e   0 < x ≤ 1 2 4 - x + 1 ,     s e   1 2 < x ≤ 1 0 ,     c a s o   c o n t r á r i o

Passo 3

Agora podemos calcular a esperança, que é dada por:

E X = ∫ - ∞ + ∞ x f x d x = ∫ 0 1 2 x . 4 x   d x + ∫ 1 2 1 x . 4 - x + 1 d x

E X = 4 x 3 3 0 1 2 + - 4 x 3 3 + 4 x 2 2 1 2 1 = 1 2

E a variância é:

V a r X = ∫ - ∞ + ∞ x - E X 2 f x d x

Calculando essa integral:

∫ 0 1 2 4 x x - 1 2 2 d x + ∫ 1 2 1 4 - x + 1 x - 1 2 2 d x =

= x 4 - 4 3 x 3 + 1 2 x 2 0 1 2 + - x 4 + 8 3 3 - 5 2 x 2 + x 1 2 1 = 1 24

Resposta

1 2

1 24

Exercícios de Livros Relacionados

A espessura, micrômetros, de um revestimento condutivo tem uma função densidade de 600 x - 2 para 100 μ mx120 μ m .Determine a média e a variância da espessura de revestimento.Se o revestimento custar
Suponha que f ( x ) = 1.5 x 2 para - 1x1 . Determine a média e a variância de X .
Suponha que uma função densidade de probabilidade do comprimento de cabos de computadores seja f ( x ) = 0.1 de 1200 a 1210 milímetros.Determine a média e o desvio-padrão do comprimento do cabo.Se as
Se o lucro de um revendedor, em unidades de $5.000, sobre um novo automóvel pode ser visto como a variável aleatória X, tendo função de densidade f x =2 ( 1 - x ) , 0x1 0 , c a s oc o n t r á r i o á
A função de densidade das medidas codificadas do afastamento das roscas de um ajuste é f x = 4 π ( 1 + x 2 ) , 0x1 0 ,c a s oc o n t r á r i o á Determine o valor esperado de X.