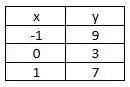
Encontre o modelo quadrático da forma que melhor se ajusta (no sentido dos mínimos quadrados) aos dados experimentais da tabela abaixo. Assinale o valor do coeficiente b.
(a) 2
(b) 3
(c) 4
(d) 5
Passo 1
Vamos tentar montar um sistema linear para achar os valores de a e b.
Substituindo os dados da tabela na fórmula
Esse sistema claramente não tem solução (a primeira e a terceira equação não são compatíveis), então vamos achar a melhor solução no sentido de mínimos quadrados.
Passo 2
Para isso, vamos precisar resolver:
Onde A é a matriz dos coeficientes do nosso sistema linear, b é o vetor do lado direito e z é a incógnita, ou seja, o vetor que possui como entradas os valores de a e b.
Escrevendo esses caras:
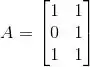
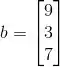
![]()
Substituindo na equação de mínimos quadrados e resolvendo:
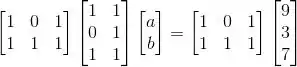
![]()
Pra resolver esse sistema, vamos montar a matriz aumentada e escalonar:
![]()
![]()
Da segunda equação, tiramos que:
Resposta
(b) 3