A equação que modela um determinado fenômeno físico é dada pela função Alguns experimentos foram realizados com os seguintes resultados:
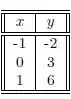
Os valores de a e b de forma a obter a melhor aproximação no sentido dos mínimos quadrados são:
(a)
(b)
(c)
(d)
Passo 1
Aparentemente essa é uma questão normal de funções, né??
Vamos substituir os dados da tabela na função:
E ver o que acontece.
Substituindo:
Ou seja, ficamos com o sistema linear:
Mas se a gente tenta resolver isso, não vamos achar solução!!
Por isso queremos uma solução aproximada e aí que entra o método dos mínimos quadrados.
Passo 2
A matriz dos coeficientes desse sistema é:
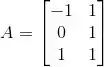
O vetor do lado direito é:
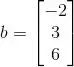
Para resolver esse sistema pelo método dos mínimos quadrados, vamos precisar resolver a seguinte equação matricial:
Onde z é vetor que tem como entradas os valores aproximados de a e b.
Vamos resolver isso:
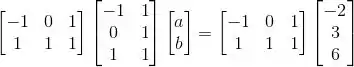
![]()
Então:
Resposta
(b)