A equação que modela um determinado fenômeno físico é dada pela função . Alguns experimentos foram realizados com os seguintes resultados:
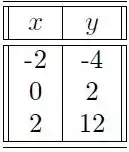
Os valores de , de forma a obter a melhor aproximação no sentido dos mínimos quadrados são:
,
,
,
Passo 1
O enunciado já até fala que é pra usar mínimos quadrados haha, então vamos lá! Bom o único problema aqui é que não temos uma matriz nem um vetor que queremos projetar pra poder usar nossa fórmula. Então temos que encontrar eles.
Montando o sistema:
Jogando isso para a forma matricial:
Agora é só jogar na fórmula e fim de papo:
Logo, a resposta é a .
Resposta
Letra